Liczba surrealistyczna - Surreal number

W matematyce The surrealistyczne numer systemu jest uporządkowany odpowiedniej klasie zawierającej liczb rzeczywistych , jak i nieskończony i liczby nieskończenie odpowiednio większą lub mniejszą wartość bezwzględną niż dodatniej liczby rzeczywistej. Surreale mają wiele wspólnych właściwości z rzeczywistymi, w tym zwykłe operacje arytmetyczne (dodawanie, odejmowanie, mnożenie i dzielenie); jako takie tworzą uporządkowane pole . Sformułowane w teorii mnogości von Neumanna-Bernaysa-Gödla , liczby surrealistyczne są uniwersalnym ciałem uporządkowanym w tym sensie, że wszystkie inne ciała uporządkowane, takie jak wymierne, rzeczywiste, funkcje wymierne , pole Levi-Civity , liczby nadrzeczywiste , a liczby hiperrzeczywiste , mogą być realizowane jako podciała surrealiów. Surreale zawierają również wszystkie liczebniki porządkowe pozaskończone ; arytmetyka na nich jest podana przez operacje naturalne . Wykazano również (w teorii mnogości von Neumanna-Bernaysa-Gödla), że maksymalne pole hiperrealne klasy jest izomorficzne z maksymalnym polem klasy surrealistycznym.

Historia koncepcji

Badania nad grą końcową Go autorstwa Johna Hortona Conwaya doprowadziły do ​​oryginalnej definicji i konstrukcji liczb surrealistycznych. Konstrukcję Conwaya przedstawiono w książce Donalda Knutha z 1974 roku Surreal Numbers: How Two Ex-Students Turn on to Pure Mathematics and Found Total Happiness . W swojej książce, która przybiera formę dialogu, Knuth ukuł termin liczby surrealistyczne dla tego, co Conway nazwał po prostu liczbami . Conway później przyjął termin Knutha i używał surreali do analizy gier w swojej książce z 1976 r. O liczbach i grach .

Odrębna droga do zdefiniowania surrealiów rozpoczęła się w 1907 roku, kiedy Hans Hahn wprowadził szereg Hahna jako uogólnienie formalnych szeregów potęgowych , a Hausdorff wprowadził pewne uporządkowane zbiory zwane η _α -zbiorami dla liczb porządkowych α i zapytał, czy jest możliwe znalezienie zgodnego uporządkowanego struktura grupy lub pola. W 1962 Alling użył zmodyfikowanej postaci szeregu Hahna do skonstruowania takich uporządkowanych ciał powiązanych z pewnymi liczbami porządkowymi α, aw 1987 pokazał, że przyjęcie α jako klasy wszystkich liczb porządkowych w jego konstrukcji daje klasę, która jest uporządkowanym ciałem izomorficznym z liczby surrealistyczne.

Jeśli surrealiści są uważani za „tylko” prawdziwe zamknięte pole o odpowiedniej wielkości klas, artykuł Allinga z 1962 r. zajmuje się przypadkiem silnie niedostępnych kardynałów, których można naturalnie uznać za właściwe klasy, odcinając kumulatywną hierarchię wszechświata o jeden stopień powyżej kardynała. Alling w związku z tym zasługuje na wielkie uznanie za odkrycie/wynalezienie surreali w tym sensie. Na surrealiach istnieje ważna dodatkowa struktura pola, która nie jest widoczna przez tę soczewkę, a mianowicie pojęcie „urodziny” i odpowiadający mu naturalny opis surrealiów w wyniku procesu wypełniania wzdłuż ich urodzin, podanego przez Conwaya. Ta dodatkowa struktura stała się podstawą współczesnego rozumienia liczb surrealistycznych, a Conwayowi przypisuje się zasługę za odkrycie surrealiów, jakie znamy dzisiaj – sam Alling w pełni przypisuje Conwayowi w artykule z 1985 roku, poprzedzającym jego książkę na ten temat.

Przegląd

W konstrukcji Conwaya liczby surrealistyczne są konstruowane etapami, wraz z porządkowaniem ≤ takim, że dla dowolnych dwóch liczb surrealistycznych a i b , a ≤ b lub b ≤ a . (Oba mogą istnieć, w takim przypadku a i b są równoważne i oznaczają tę samą liczbę.) Każda liczba jest utworzona z uporządkowanej pary podzbiorów liczb już skonstruowanych: dane podzbiory L i R liczb takie, że wszystkie elementy L są ściśle mniej niż wszystkie elementy R , to para { L | R } reprezentuje liczbę pośrednią w wartości między wszystkimi członkami L i wszystkimi członkami R .

Różne podzbiory mogą ostatecznie zdefiniować tę samą liczbę: { L | R } i { L′ | R′ } może zdefiniować tę samą liczbę, nawet jeśli L ≠ L′ i R ≠ R′ . (Podobne zjawisko występuje, gdy liczby wymierne definiuje się jako iloraz liczb całkowitych: 1/2 i 2/4 to różne reprezentacje tej samej liczby wymiernej.) Ściślej mówiąc, liczby surrealistyczne są klasami równoważności reprezentacji postaci { L | R }, które oznaczają ten sam numer.

W pierwszym etapie budowy nie istnieją wcześniej liczby, więc jedyną reprezentacją musi być zbiór pusty: { | } . Ta reprezentacja, gdzie L i R są puste, nazywa się 0. Kolejne etapy dają formy takie jak

{ 0 | } = 1

{ 1 | } = 2

{ 2 | } = 3

oraz

{ | 0} = −1

{ | -1 } = -2

{ | -2 } = -3

Liczby całkowite są więc zawarte w liczbach surrealistycznych. (Powyższe tożsamości są definicjami, w tym sensie, że prawa strona jest nazwą dla lewej strony. To, że nazwy są rzeczywiście odpowiednie, będzie oczywiste, gdy zostaną zdefiniowane operacje arytmetyczne na liczbach surrealistycznych, jak w sekcji poniżej ). Podobnie reprezentacje takie jak

{ 0 | 1} = 1/2

{ 0 | 1/2} = 1/4

{ 1/2 | 1} = 3/4

powstają, tak że wymierne liczby dwuczłonowe (liczby wymierne, których mianownikami są potęgi 2), są zawarte w liczbach surrealistycznych.

Po nieskończonej liczbie etapów dostępne stają się nieskończone podzbiory, tak że dowolna liczba rzeczywista a może być reprezentowana przez { L _a | R }, gdzie L jest zbiorem wszystkich dwójkowym wymiernych poniżej i R jest zbiorem wszystkich dwójkowym wymiernych większych niż (przypominający DEDEKIND cięcia ). Tak więc liczby rzeczywiste są również osadzone w surrealiach.

Istnieją również reprezentacje takie jak

{0,1,2,3,... | } =

{ 0 | 1, 1/2, 1/4, 1/8, ... } = ε

gdzie ω jest liczbą nieskończoną większą niż wszystkie liczby całkowite, a ε jest nieskończenie małą liczbą większą niż 0, ale mniejszą niż jakakolwiek dodatnia liczba rzeczywista. Co więcej, standardowe operacje arytmetyczne (dodawanie, odejmowanie, mnożenie i dzielenie) można rozszerzyć na te liczby nierzeczywiste w taki sposób, że zbiór liczb surrealistycznych zamienia się w uporządkowane pole, tak że można mówić o 2ω lub ω − 1 i tak dalej.

Budowa

Liczby Nadrzeczywiste są skonstruowane indukcyjnie w równoważnych grup z parami zestawów numerów surrealistycznych, ograniczonej przez warunkiem, że każdy element pierwszego zestawu jest mniejszy niż każdy element drugiego zestawu. Konstrukcja składa się z trzech współzależnych części: reguły konstrukcji, reguły porównania i reguły równoważności.

Formularze

Forma jest parę zestawów liczb surrealistycznych, zwany jego lewy zestaw i jego prawo zestaw . Forma z lewym zbiorem L i prawym zbiorem R jest zapisana { L | R } . Gdy L i R są podane jako listy elementów, nawiasy wokół nich są pomijane.

Pustym zbiorem może być jeden lub oba lewy i prawy zbiór formularza. Forma { { } | { } } z lewą i prawą ustawioną pustym jest również zapisywane { | } .

Formy liczbowe i ich klasy równoważności

Zasada budowy

Forma { L | R } jest liczbowe, jeśli przecięcie L i R jest zbiorem pustym, a każdy element R jest większy niż każdy element L , zgodnie z relacją kolejności ≤ podaną przez poniższą regułę porównania.

Formy liczbowe są umieszczone w klasach równoważności; każda taka klasa równoważności jest liczbą surrealistyczną . Elementy lewego i prawego zbioru formy są wyciągane z uniwersum liczb surrealistycznych (nie form , ale ich klas równoważności ).

Zasada równoważności

Dwie formy liczbowe x i y są formami o tej samej liczbie (leżą w tej samej klasie równoważności) wtedy i tylko wtedy, gdy x ≤ y i y ≤ x .

Związek kolejność musi być antysymetryczny , czyli musi mieć taką właściwość, że x = y (to znaczy x ≤ y i y ≤ x oba prawda) tylko wtedy, gdy x i y są tym samym obiektem. Nie jest tak w przypadku form liczb surrealistycznych , ale jest prawdziwe przy konstrukcji liczb surrealistycznych (klasy równoważności).

Klasa równoważności zawierająca { | } jest oznaczony jako 0; innymi słowy, { | } jest formą surrealistycznej liczby 0.

Zamówienie

Rekurencyjną definicję liczb surrealistycznych uzupełnia definicja porównania:

Dane postaci liczbowe x = { X _L | X _R } i y = { Y _L | Y _R }, x ≤ y wtedy i tylko wtedy, gdy:

• Nie ma x _L ∈ X _L takiego, że y ≤ x _L (każdy element w lewej części x jest mniejszy niż y ), oraz
• Nie ma y _R ∈ Y _R takiego, że y _R ≤ x (każdy element w prawej części y jest większy niż x ).

Porównanie y ≤ c między formą y i liczbą surrealistyczną c jest wykonywane przez wybranie formy z z klasy równoważności c i ocenę y ≤ z ; i podobnie dla c ≤ x i dla porównania b ≤ c między dwiema liczbami surrealistycznymi.

Wprowadzenie

Ta grupa definicji ma charakter rekurencyjny i wymaga pewnej formy indukcji matematycznej w celu zdefiniowania wszechświata obiektów (form i liczb), które w nich występują. Jedynymi liczbami surrealistycznymi osiągalnymi przez skończoną indukcję są ułamki dwójkowe ; szerszy wszechświat jest osiągalny dzięki pewnej formie indukcji pozaskończonej .

Zasada indukcyjna

• Istnieje pokolenie S ₀ = { 0 }, w którym 0 składa się z pojedynczej postaci { | }.
• Biorąc pod uwagę dowolną liczbę porządkową n , pokolenie S _n jest zbiorem wszystkich liczb surrealistycznych, które są generowane przez regułę konstrukcji z podzbiorów .${\ Displaystyle \ filiżanka _ {i <n} S_ {i}}$

Przypadek podstawowy jest w rzeczywistości szczególnym przypadkiem reguły indukcji, gdzie 0 jest traktowane jako etykieta dla „najmniejszej liczby porządkowej”. Ponieważ nie istnieje S _i z i < 0, wyrażenie jest zbiorem pustym; jedynym podzbiorem zbioru pustego jest zbiór pusty, a zatem S ₀ składa się z pojedynczej formy surrealistycznej { | } leżący w jednej klasie równoważności 0. ${\ Displaystyle \ filiżanka _ {i <0} S_ {i}}$

Dla każdej skończonej liczby porządkowej n , S _n jest uporządkowane zgodnie z porządkiem wywołanym przez regułę porównania na liczbach surrealistycznych.

Pierwsza iteracja reguły indukcji daje trzy formy liczbowe { | 0 } < { | } < { 0 | } (forma { 0 | 0 } jest nieliczbowa, ponieważ 0≤0). Klasa równoważności zawierająca { 0 | } jest oznaczony 1, a klasa równoważności zawierająca { | 0 } jest oznaczone jako -1. Te trzy etykiety mają szczególne znaczenie w aksjomatach definiujących pierścień ; są to tożsamość addytywna (0), tożsamość multiplikatywna (1) i addytywna odwrotność 1 (-1). Zdefiniowane poniżej operacje arytmetyczne są zgodne z tymi etykietami.

Dla każdego i < n , ponieważ każda ważna forma w S _i jest również poprawną formą w S _n , wszystkie liczby w S _i pojawiają się również w S _n (jako nadzbiory ich reprezentacji w S _i ). (Wyrażenie suma zbioru pojawia się w naszej regule konstrukcji zamiast prostszej postaci S _{n -1} , tak więc definicja ma sens również wtedy, gdy n jest limitem porządkowym .) Liczby w S _n, które są nadzbiorem pewnej liczby w S _i mówi się, że zostały odziedziczone z pokolenia i . Najmniejsza wartość α, dla której dana liczba surrealistyczna występuje w S _α, nazywa się jej urodzinami . Na przykład data urodzenia 0 to 0, a data urodzenia -1 to 1.

Druga iteracja reguły konstrukcji daje następującą kolejność klas równoważności:

{ | -1 } = { | -1, 0} = { | -1, 1 } = { | -1, 0, 1 }

< { | 0} = { | 0, 1 }

< { -1 | 0 } = { -1 | 0, 1 }

< { | } = { -1 | } = { | 1 } = { -1 | 1 }

< { 0 | 1 } = { -1, 0 | 1 }

< { 0 | } = { -1, 0 | }

< { 1 | } = { 0, 1 | } = { -1, 1 | } = { -1, 0, 1 | }

Porównanie tych klas równoważności jest spójne, niezależnie od wyboru formy. Następują trzy obserwacje:

1. S ₂ zawiera cztery nowe liczby surrealistyczne. Dwie zawierają formy ekstremalne: { | -1, 0, 1 } zawiera wszystkie liczby z poprzednich pokoleń w swoim prawym zbiorze, a { -1, 0, 1 | } zawiera wszystkie liczby z poprzednich pokoleń w swoim lewym zestawie. Pozostałe mają formę, która dzieli wszystkie liczby z poprzednich pokoleń na dwa niepuste zestawy.
2. Każda liczba surrealistyczna x, która istniała w poprzednim „pokoleniu”, istnieje również w tym pokoleniu i zawiera co najmniej jedną nową formę: podział wszystkich liczb innych niż x z poprzednich pokoleń na zbiór lewy (wszystkie liczby mniejsze niż x ) i a prawy zestaw (wszystkie liczby większe niż x ).
3. Klasa równoważności liczby zależy tylko od maksymalnego elementu jej lewego zbioru i minimalnego elementu prawego zbioru.

Nieformalne interpretacje { 1 | } i { | −1 } to odpowiednio „liczba tuż po 1” i „liczba tuż przed −1”; ich klasy równoważności są oznaczone jako 2 i -2. Nieformalne interpretacje { 0 | 1 } i { -1 | 0 } to odpowiednio „liczba w połowie między 0 a 1” i „liczba w połowie między -1 i 0”; ich klasy równoważności są oznaczone jako ¹ / ₂ i − ¹ / ₂ . Etykiety te będą również uzasadnione poniższymi zasadami surrealistycznego dodawania i mnożenia.

Klasy równoważności na każdym etapie n indukcji można scharakteryzować za pomocą ich n - kompletnych form (każda zawierająca możliwie najwięcej elementów poprzednich generacji w swoich lewych i prawych zbiorach). Albo ta pełna forma zawiera każdą liczbę z poprzednich pokoleń w swoim lewym lub prawym zestawie, w którym to przypadku jest to pierwsze pokolenie, w którym ta liczba występuje; lub zawiera wszystkie liczby z poprzednich pokoleń oprócz jednej, w tym przypadku jest to nowa forma tej jednej liczby. Zachowujemy etykiety z poprzedniej generacji dla tych „starych” numerów i zapisujemy powyższą kolejność, używając starych i nowych etykiet:

-2 <-1 <- ¹ / ₂ <0 < ¹ / ₂ <1 <2.

Trzecia obserwacja rozciąga się na wszystkie liczby surrealistyczne ze skończonymi zbiorami lewego i prawego. (Dla nieskończonych lewych lub prawych zbiorów jest to ważne w zmienionej formie, ponieważ nieskończone zbiory mogą nie zawierać elementu maksymalnego lub minimalnego.) Liczba { 1, 2 | 5, 8 } jest zatem równoważne { 2 | 5}; można ustalić, że są to formy 3, korzystając z własności urodzin , co jest konsekwencją powyższych reguł.

Urodziny nieruchomości

Forma x = { L | R } występujący w pokoleniu n reprezentuje liczbę odziedziczoną z wcześniejszego pokolenia i < n wtedy i tylko wtedy, gdy w S _i istnieje liczba większa niż wszystkie elementy L i mniejsza niż wszystkie elementy R . (Innymi słowy, jeśli L i R są już oddzielone liczbą utworzoną na wcześniejszym etapie, to x nie reprezentuje nowej liczby, ale już skonstruowaną.) Jeśli x reprezentuje liczbę z dowolnego pokolenia wcześniejszego niż n , istnieje najmniej takie pokolenie i , i dokładnie jedna liczba c z tą najmniejszą i , ponieważ jej data urodzenia leży między L i R ; x jest formą tego c . Innymi słowy, leży w klasie równoważności w S _n, która jest nadzbiorem reprezentacji c w generacji i .

Arytmetyka

Dodawanie, negacja (odwrotność dodawania) i mnożenie form liczb surrealistycznych x = { X _L | X _R } i y = { Y _L | Y _R } są zdefiniowane przez trzy formuły rekurencyjne.

Negacja

Negacja danej liczby x = { X _L | X _R } jest zdefiniowany przez

${\ Displaystyle -x = - \ {X_ {L} | X_ {R} \} = \ {-X_ {R} | - X_ {L} \}}$,

gdzie negacja zbioru S liczb jest dana przez zbiór zanegowanych elementów zbioru S :

${\displaystyle -S=\{-s:s\w S\}}$.

Formuła ta polega na negacji liczb surrealistycznych występujących w lewym i prawym zbiorze x , co należy rozumieć jako wynik wyboru formy liczby, oceny negacji tej formy i przyjęcia klasy równoważności otrzymanej Formularz. Ma to sens tylko wtedy, gdy wynik jest taki sam, niezależnie od wyboru formy operandu. Można to udowodnić indukcyjnie, wykorzystując fakt, że liczby występujące w X _L i X _R są losowane z pokoleń wcześniejszych niż ta, w której po raz pierwszy występuje forma x , oraz obserwując przypadek szczególny:

${\ Displaystyle -0 = - \ {| \} = \ {| \} = 0}$.

Dodatek

Definicja dodawania jest również formułą rekurencyjną:

${\ Displaystyle x + y = \ {X_ {L} | X_ {R} \} + \ {Y_ {L} | Y_ {R} \} = \ {X_ {L} + Y, x + Y_ {L} |X_{R}+y,x+Y_{R}\}}$,

gdzie

${\ Displaystyle X + y = \ {x + y: x \ w X \}, x + Y = \ {x + y: y \ w Y \}}$.

Ta formuła obejmuje sumy jednego z oryginalnych operandów i surrealistyczną liczbę wylosowaną z lewego lub prawego zestawu drugiego. Należy je rozumieć jako wynik wyboru formy operandu liczbowego, wykonania sumy dwóch form i przyjęcia klasy równoważności formy wynikowej. Ma to sens tylko wtedy, gdy wynik jest taki sam, niezależnie od wyboru postaci operandu liczbowego. Można to również udowodnić indukcyjnie w przypadkach specjalnych:

0 + 0 = { | } + { | } = { | } = 0

x + 0 = x + { | } = { X _L + 0 | X _R + 0 } = { X _L | X _R } = x

0 + y = { | } + y = { 0 + Y _L | 0 + Y _R } = { Y _L | Y _R } = Y

Te dwa ostatnie przypadki są same w sobie udowodnione indukcyjnie.

Mnożenie

Rekurencyjna formuła mnożenia zawiera wyrażenia arytmetyczne obejmujące operandy i ich lewe i prawe zestawy, takie jak wyrażenie, które pojawia się w lewym zbiorze iloczynu x i y . Należy przez to rozumieć zbiór liczb surrealistycznych wynikający z wybrania jednej liczby z każdego zestawu, który pojawia się w wyrażeniu i oceny wyrażenia na tych liczbach. (W każdej indywidualnej ocenie wyrażenia z każdego zestawu wybierana jest tylko jedna liczba, która jest zastępowana w każdym miejscu, w którym ten zestaw pojawia się w wyrażeniu). ${\ Displaystyle X_ {R} y + xY_ {R}-X_ {R} Y_ {R}}$

To z kolei zależy od umiejętności (a) pomnożenia par liczb surrealistycznych wylosowanych z lewego i prawego zbioru x i y w celu uzyskania liczby surrealistycznej i zanegowania wyniku; (b) pomnóż liczbę surrealistyczną z postaci x lub y i liczbę surrealistyczną wylosowaną z lewego lub prawego zbioru drugiego argumentu, aby otrzymać liczbę surrealistyczną; oraz (c) dodać otrzymane liczby surrealistyczne. To znowu dotyczy specjalnych przypadków, tym razem zawierających 0 = { | }, tożsamość multiplikatywna 1 = { 0 | }, a jego dodatek odwrotność -1 = { | 0}.

${\ Displaystyle {\ zacząć {wyrównany} xy = \ {X_ {L} | X_ {R} \} \ {Y_ {L} | Y_ {R} \} \ \ & = \ lewo \ {X_ {L} y +xY_{L}-X_{L}Y_{L},X_{R}y+xY_{R}-X_{R}Y_{R}|X_{L}y+xY_{R}-X_{L} Y_{R},xY_{L}+X_{R}y-X_{R}Y_{L}\right\}\\\end{aligned}}}$

Podział

Definicja dzielenia odbywa się w kategoriach odwrotności i mnożenia:

${\ Displaystyle {\ Frac {x} {y}} = x \ lewo ({\ Frac {1} {y}} \ prawej)}$

gdzie

${\ Displaystyle {\ Frac {1} {y}} = {\ Bigg \ {} 0 {\ Frac {1 + (y_ {R}-y) ({\ Frac {1} {y}}) _ { L}}{r_{R}}},{\frac {1+(r_{L}-r)({\frac {1}{r}})_{R}}{r_{L}}}{ \Bigg |}{\frac {1+(y_{L}-y)({\frac {1}{y}})_{L}}{y_{L}}},{\frac {1+( y_{R}-y)({\frac {1}{y}})_{R}}{y_{R}}}{\Bigg \}}}$

dla pozytywnych . W formule dozwolone są tylko wartości dodatnie , a wszelkie niedodatnie wyrażenia są ignorowane (i zawsze są dodatnie). Ta formuła obejmuje nie tylko rekursję w sensie możliwości dzielenia przez liczby z lewego i prawego zbioru , ale także rekurencję polegającą na tym, że członkowie lewego i prawego zbioru samego siebie. jest zawsze członkiem lewego zbioru i można go użyć do znalezienia większej liczby terminów w sposób rekurencyjny. Na przykład, jeśli , to wiemy, że lewy wyraz woli będzie . To z kolei oznacza, że jest to właściwe określenie. Oznacza to termin lewicowy. Oznacza to, że będzie to właściwe określenie. Kontynuując, daje to . ${\textstyle y}$${\textstyle y_{L}}$${\textstyle y_{R}}$${\textstyle y}$${\textstyle {\frac {1}{y}}}$${\textstyle 0}$${\textstyle {\frac {1}{y}}}$${\textstyle y=3=\{2|\}}$${\textstyle {\frac {1}{3}}}$${\textstyle 0}$${\textstyle {\frac {1+(2-3)0}{2}}=1/2}$${\textstyle {\frac {1+(2-3)\left({\frac {1}{2}}\right)}{2}}={\frac {1}{4}}}$${\textstyle {\frac {1+(2-3)\left({\frac {1}{4}}\right)}{2}}={\frac {3}{8}}}$${\textstyle {\frac {1}{3}}=\{0,{\frac {1}{4}},{\frac {5}{16}},\ldots |{\frac {1}{ 2}},{\frac {3}{8}},\ldots \}}$

Negatywne , jest podane przez . Jeśli , to jest niezdefiniowane. ${\textstyle y}$${\textstyle {\frac {1}{y}}}$${\textstyle {\frac {1}{y}}=-\left({\frac {1}{-y}}\right)}$${\ Displaystyle y = 0}$${\displaystyle {\frac {1}{y}}}$

Spójność

Można wykazać, że definicje negacji, dodawania i mnożenia są spójne w tym sensie, że:

• Dodawanie i negacja są definiowane rekursywnie w kategoriach „prostszych” kroków dodawania i negacji, tak że operacje na liczbach z datą urodzenia n zostaną ostatecznie wyrażone w całości w kategoriach operacji na liczbach o urodzinach mniejszych niż n ;
• Mnożenie jest definiowane rekurencyjnie w kategoriach dodawania, negacji i „prostszych” kroków mnożenia, tak że iloczyn liczb z datą urodzenia n będzie ostatecznie wyrażony w całości jako sumy i różnice iloczynów liczb z datą urodzenia mniejszą niż n ;
• Dopóki operandy są dobrze zdefiniowanymi surrealistycznymi formami liczbowymi (każdy element lewego zestawu jest mniejszy niż każdy element prawego zestawu), wyniki są ponownie dobrze zdefiniowanymi surrealistycznymi formami liczbowymi;
• Operacje można rozszerzyć na liczby (klasy równoważności form): wynik zanegowania x lub dodania lub pomnożenia x i y będzie reprezentował tę samą liczbę niezależnie od wyboru formy x i y ; oraz
• Operacje te są zgodne z aksjomatami asocjatywności, przemienności, odwrotności addytywnej i rozdzielności w definicji pola o identyczności addytywnej 0 = { | } i tożsamość multiplikatywna 1 = { 0 | }.

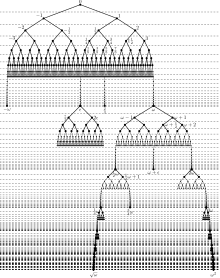
Dzięki tym regułom można teraz zweryfikować, czy liczby znalezione w pierwszych kilku pokoleniach zostały odpowiednio oznakowane. Zasada konstrukcji jest powtarzana, aby uzyskać więcej pokoleń surreali:

S ₀ = { 0 }

S ₁ = { -1 < 0 < 1 }

S ₂ = {-2 <-1 <- ¹ / ₂ <0 < ¹ / ₂ <1 <2}

S ₃ = {-3 <-2 <- ³ / ₂ <-1 <- ³ / ₄ <- ¹ / ₂ <- ¹ / ₄ <0 < ¹ / ₄ < ¹ / ₂ < ³ / ₄ <1 < ³ / ₂ < 2 < 3 }

S ₄ = { -4 < -3 < ... < ^-1 / ₈ < 0 < ¹ / ₈ < ¹ / ₄ < ³ / ₈ < ¹ / ₂ < ⁵ / ₈ < ³ / ₄ < ⁷ / ₈ < 1 < ⁵ / ₄ < ³ / ₂ < ⁷ / ₄ < 2 < ⁵ / ₂ < 3 < 4 }

Zamknięcie arytmetyczne

Dla każdej liczby naturalnej (skończonej liczby porządkowej) n , wszystkie liczby generowane w S _n są ułamkami dwójkowymi , tj. można je zapisać jako ułamek nierozkładalny, gdzie a i b są liczbami całkowitymi i 0 ≤ b < n . ${\ Displaystyle {\ Frac {a} {2 ^ {b}}}}$

Zbiór wszystkich liczb surrealistycznych, które są generowane w pewnym S _n dla skończonego n można określić jako S _* = . Można utworzyć trzy klasy S ₀ = { 0 }, S ₊ = i S ₋ = , z których S _* jest sumą. Żaden pojedynczy S _{n nie} jest zamknięty przy dodawaniu i mnożeniu (z wyjątkiem S ₀ ), ale S _* jest; jest to podgrupa wymiernych, składająca się ze wszystkich ułamków dwuczłonowych. ${\ Displaystyle \ filiżanka _ {n \ w N} S_ {n}}$${\ Displaystyle \ {x \ w S_ {*}: x> 0 \}}$${\ Displaystyle \ {x \ w S_ {*}: x <0 \}}$

Istnieją nieskończone liczby porządkowe β, dla których zbiór liczb surrealistycznych z datą urodzenia mniejszą niż β jest domknięty w ramach różnych operacji arytmetycznych. Dla dowolnej liczby porządkowej α zbiór liczb surrealistycznych z datą urodzenia mniejszą niż β = ω ^α (przy użyciu potęg ω ) jest domknięty przez dodawanie i tworzy grupę; na urodziny krótsze niż ω ^{ω α} jest zamykane przez mnożenie i tworzy pierścień; a dla daty urodzin mniejszej niż (porządkowa) liczba epsilon ε _α jest zamknięta na odwrotność mnożnika i tworzy pole. Te ostatnie zbiory są również zamknięte pod funkcją wykładniczą zdefiniowaną przez Kruskala i Gonshora.

Jednak zawsze można skonstruować liczbę surrealistyczną, która jest większa niż jakikolwiek element zbioru surrealiów (poprzez uwzględnienie zbioru po lewej stronie konstruktora), a zatem zbiór liczb surrealistycznych jest odpowiednią klasą . Swoim porządkowaniem i operacjami algebraicznymi tworzą one ciało uporządkowane , z zastrzeżeniem, że nie tworzą zbioru . W rzeczywistości jest to bardzo szczególne uporządkowane pole: największe. Każde inne uporządkowane pole można osadzić w surrealiach. Klasę wszystkich liczb surrealistycznych oznaczono symbolem . ${\ Displaystyle \ mathbf {nie}}$

nieskończoność

Zdefiniuj S _ω jako zbiór wszystkich liczb surrealistycznych generowanych przez regułę konstrukcji z podzbiorów S _* . (Jest to ten sam krok indukcyjny co poprzednio, ponieważ liczba porządkowa ω jest najmniejszą liczbą porządkową, która jest większa od wszystkich liczb naturalnych; jednak suma zbioru występująca w kroku indukcyjnym jest teraz nieskończoną sumą zbiorów skończonych, a więc ten krok może być wykonane tylko w teorii mnogości, która pozwala na taki związek.) W S _ω występuje unikalna nieskończenie duża liczba dodatnia :

${\ Displaystyle \ omega = \ {S_ {*} | \} = \ {1,2,3,4, ... | \}.}$

S _ω zawiera również obiekty, które można zidentyfikować jako liczby wymierne . Na przykład -pełna forma ułamka ¹ / ₃ jest dana przez:

${\ Displaystyle {\ tfrac {1}{3}} = \ {y \ w S_ {*}: 3 lata <1 | r \ w S_ {*}: 3 lata> 1 \}}$.

Produkt tej postaci ¹ / ₃ z każdej formy 3 jest formą którego lewy zestaw zawiera tylko liczby jest mniejszy niż 1, a których odpowiedni zestaw zawiera tylko liczby większe niż 1; właściwość urodzin oznacza, że ​​ten produkt ma formę 1.

Nie tylko wszystkie pozostałe liczby wymierne występują w S _ω ; pozostałe skończone liczby rzeczywiste też. Na przykład,

${\ Displaystyle \ pi = \ {3, {\ Frac {25} {8}}, {\ Frac {201} {64}}, ... | 4, {\ Frac {7} {2}}, { \frac {13}{4}},{\frac {51}{16}},...\}}$.

Jedyne nieskończoności w S _ω to ω i −ω; ale wśród liczb rzeczywistych w S _ω są inne liczby nierzeczywiste . Rozważ najmniejszą liczbę dodatnią w S _ω :

${\ Displaystyle \ varepsilon = \ {S_ {-} \ filiżanka S_ {0} | S_ {+} \} = \ {0 | 1, {\ tfrac {1} {2}} {\ tfrac {1} { 4}},{\tfrac {1}{8}},...\}=\{0|y\w S_{*}:y>0\}}$.

Ta liczba jest większa od zera, ale mniejsza niż wszystkie dodatnie ułamki dwudniowe. Jest to zatem liczba nieskończenie mała, często oznaczana jako ε. -kompletna forma ε (odpowiednio -ε) jest taka sama jak ω-kompletna forma 0, z wyjątkiem tego, że 0 jest zawarte w lewym (odpowiednio prawym) zbiorze. Jedynymi „czystymi” nieskończenie małymi w S _ω są ε i jego odwrotność addytywna -ε; dodanie ich do dowolnego ułamka dwuczłonowego y daje liczby y ±ε, które również leżą w S _ω .

Zależność między ω i ε można wyznaczyć mnożąc poszczególne ich formy do uzyskania:

ω · ε = { ε · S ₊ | ω · S ₊ + S _* + ε · S _* }.

Wyrażenie to jest dobrze zdefiniowane tylko w teorii mnogości, która dopuszcza indukcję pozaskończoną aż do . W takim układzie można wykazać, że wszystkie elementy lewego zbioru ω · ε są dodatnimi nieskończenie małymi, a wszystkie elementy prawego zbioru są dodatnimi nieskończonościami, a zatem ω · ε jest najstarszą dodatnią liczbą skończoną, tj. 1 . W konsekwencji, ${\ Displaystyle S_ {\ omega ^ {2}}}$

¹ / _ε = .

Niektórzy autorzy systematycznie używają ω ^-1 zamiast symbolu ε.

Zawartość S _ω

Biorąc pod uwagę dowolny x = { L | R } w S _ω , dokładnie jedno z poniższych jest prawdziwe:

• L i R są oba puste, w takim przypadku x = 0;
• R jest puste i pewna liczba całkowita n ≥0 jest większa niż każdy element L , w którym to przypadku x jest równe najmniejszej takiej liczbie całkowitej n ;
• R jest puste i żadna liczba całkowita n nie jest większa niż każdy element L , w takim przypadku x równa się +ω;
• L jest puste i pewna liczba całkowita n ≤0 jest mniejsza niż każdy element R , w którym to przypadku x równa się największej takiej liczbie całkowitej n ;
• L jest puste i żadna liczba całkowita n nie jest mniejsza niż każdy element R , w którym to przypadku x równa się -ω;
• L i R są niepuste i:
  • Niektóre ułamki dwójkowe y są „ściśle między” L i R (większe niż wszystkie elementy L i mniejsze niż wszystkie elementy R ), w którym to przypadku x równa się najstarszemu takiemu ułamkowi dwójkowemu y ;
  • Żaden ułamek dwudniowy y nie leży ściśle między L i R , ale pewien ułamek dwudniowy jest większy lub równy wszystkim elementom L i mniejszy niż wszystkie elementy R , w którym to przypadku x równa się y + ε;${\ Displaystyle y \ w L}$
  • Żaden ułamek dwójkowy y nie leży ściśle pomiędzy L i R , ale pewien ułamek dwójkowy jest większy niż wszystkie elementy L i mniejszy lub równy wszystkim elementom R , w którym to przypadku x równa się y- ε;${\ Displaystyle y \ w R}$
  • Każdy ułamek dwójkowy jest albo większy niż jakiś element R, albo mniejszy niż jakiś element L , w którym to przypadku x jest pewną liczbą rzeczywistą, która nie ma reprezentacji jako ułamek dwójkowy.

S _ω nie jest ciałem algebraicznym, ponieważ nie jest domknięty pod działaniami arytmetycznymi; rozważmy ω+1, którego forma nie leży w żadnej liczbie w S _ω . Maksymalny podzbiór S _ω, który jest zamknięty (skończonym szeregiem) operacji arytmetycznych, jest ciałem liczb rzeczywistych, otrzymanym przez pominięcie nieskończoności ±ω, nieskończenie małych ±ε i nieskończenie małych sąsiadów y ±ε każdego niezerowego ułamka dwójkowego y . ${\ Displaystyle \ {1,2,3,4, ... | \} + \ {0 | \} = \ {1,2,3,4,..., \ omega | \}}$

Taka konstrukcja liczb rzeczywistych różni się od DEDEKIND nacięć w standardowej analizie na tym, że wychodzi się z dwójkowym frakcji zamiast ogólnych wymiernych i naturalnie identyfikuje każdy dwójkowym frakcji w S _Ohm z jego form z poprzednich pokoleń. (Formy ω-zupełne elementów rzeczywistych S _ω odpowiadają jeden do jednego z liczbami rzeczywistymi uzyskanymi przez cięcia Dedekinda, pod warunkiem, że liczby rzeczywiste Dedekinda odpowiadające liczbom wymiernym są reprezentowane przez postać, w której punkt cięcia jest pominięty zarówno z lewego, jak i prawego zestawu). są one jedynie podzbiór Q z S _ω zawierający wszystkie elementy x tak, że x b = jakiegoś A i niektóre niezerową , b , które są sporządzane z S _* . Pokazując, że Q jest domknięte w ramach indywidualnych powtórzeń surrealistycznych operacji arytmetycznych, można pokazać, że jest to pole; i pokazując, że każdy element Q jest osiągalny z S _* przez skończony szereg (w rzeczywistości nie dłuższy niż dwa) operacji arytmetycznych, w tym inwersję multiplikatywną , można pokazać, że Q jest ściśle mniejsze niż podzbiór S _ω utożsamiany z liczbami rzeczywistymi .

Zbiór S _ω ma taką samą moc jak liczby rzeczywiste R . Można to wykazać poprzez wykazanie suriekcją mapowania z S _Ohm do zamkniętego urządzenia przedział I z R i vice versa. Mapowanie S _ω na I jest rutyną; mapuje liczby mniejsze lub równe ε (włącznie z -ω) na 0, liczby większe lub równe 1-ε (włącznie z ω) na 1 oraz liczby między ε i 1-ε na ich odpowiedniki w I (odwzorowywanie nieskończenie małych sąsiadów y ±ε każdego ułamka dwójkowego y , wraz z samym y , do y ). Aby zmapować I na S _ω , _zmapuj (otwartą) środkową trzecią (1/3, 2/3) I na { | } = 0; środkowa tercja (7/9, 8/9) górnej tercji do { 0 | } = 1; i tak dalej. To odwzorowuje niepusty otwarty przedział I na każdy element S _* , monotonicznie. Reszta I składa się ze zbioru Cantora 2 ^ω , którego każdy punkt jest jednoznacznie identyfikowany przez podział interwałów tercji środkowej na zbiory lewy i prawy, odpowiadający dokładnie formie { L | R } w S _ω . To umieszcza zestaw Cantora w korespondencji jeden do jednego z zestawem liczb surrealistycznych z datą urodzin ω.

Indukcja nieskończona

Kontynuacja wykonywania indukcji pozaskończonej poza S _ω daje więcej liczb porządkowych α, z których każda jest reprezentowana jako największa liczba surrealistyczna mająca urodziny α. (Jest to zasadniczo definicja liczb porządkowych wynikających z indukcji pozaskończonej.) Pierwsza taka liczba porządkowa to ω+1 = { ω | }. W generacji ω+1 jest jeszcze jedna dodatnia nieskończona liczba:

ω−1 = { 1, 2, 3, 4, ... | }.

Liczba surrealistyczna ω-1 nie jest liczbą porządkową; liczba porządkowa ω nie jest następcą żadnej liczby porządkowej. Jest to liczba surrealistyczna z datą urodzin ω+1, oznaczoną jako ω−1 na podstawie tego, że pokrywa się z sumą ω = { 1, 2, 3, 4, ... | } i -1 = { | 0}. Podobnie, są dwie nowe nieskończenie małe liczby w generacji ω+1:

2ε = ε + ε = { ε | 1 + ε, ¹ / ₂ + ε, ¹ / ₄ + ε, ¹ / ₈ + ε, ...} i

ε / 2 = ε · ¹ / ₂ = {0 | ε}.

W późniejszym etapie indukcji pozaskończonej istnieje liczba większa niż ω+ k dla wszystkich liczb naturalnych k :

2ω = ω + ω = { ω+1, ω+2, ω+3, ω+4,... | }

Liczba ta może być oznaczona jako ω + ω zarówno dlatego, że jej data urodzenia to ω + ω (pierwsza liczba porządkowa nieosiągalna od ω przez operację następnika), jak i dlatego, że pokrywa się z surrealistyczną sumą ω i ω; może być również oznaczony jako 2ω, ponieważ pokrywa się z iloczynem ω = { 1, 2, 3, 4, ... | } i 2 = { 1 | }. Jest to druga granica porządkowa; osiągnięcie go od ω poprzez etap konstrukcyjny wymaga indukcji pozaskończonej na . Wiąże się to z nieskończoną sumą zbiorów nieskończonych, która jest „silniejszą” operacją teoretyczną mnogości niż wymagana poprzednia indukcja pozaskończona. ${\ Displaystyle \ bigcup _ {k <\ omega} S_ {\ omega + k}}$

Zauważ, że konwencjonalne dodawanie i mnożenie liczb porządkowych nie zawsze pokrywa się z tymi operacjami na ich surrealistycznych reprezentacjach. Suma liczb porządkowych 1 + ω równa się ω, ale suma surrealistyczna jest przemienna i daje 1 + ω = ω + 1 > ω. Dodawanie i mnożenie liczb surrealistycznych związanych z porządkowymi pokrywa się z naturalną sumą i naturalnym iloczynem liczb porządkowych.

Tak jak 2ω jest większe niż ω + n dla dowolnej liczby naturalnej n , istnieje liczba surrealistyczna ω/2, która jest nieskończona, ale mniejsza niż ω − n dla dowolnej liczby naturalnej n . Oznacza to, że ω/2 jest zdefiniowane przez

ω/2 = { S _* | ω − S _* }

gdzie po prawej stronie notacja x − Y oznacza { x − y  : y w Y }. Można go zidentyfikować jako iloczyn ω i postaci { 0 | 1} o ¹ / ₂ . Data urodzenia ^ω / ₂ to limit porządkowy ω2.

Potęgi ω i postać normalna Conwaya

Aby sklasyfikować „rzędy” nieskończonych i nieskończenie małych liczb surrealistycznych, znanych również jako klasy archimedesowe , Conway powiązany z każdą liczbą surrealistyczną x liczba surrealistyczna

• ω ^x = { 0, r ω ^{x _L} | s ω ^{x _R} },

gdzie r i s mieszczą się w zakresie dodatnich liczb rzeczywistych. Jeśli x < y wtedy ω ^y jest „nieskończenie większe” niż ω ^x , w tym sensie , że jest większe niż r ω ^x dla wszystkich liczb rzeczywistych r . Uprawnienia ω również spełniają warunki

• ω ^x ω ^Y = ω ^{x + y} ,
• ω ^{− x} = 1/ω ^x ,

więc zachowują się tak, jak można by oczekiwać, że będą się zachowywać władze.

Każda potęga ω ma również odkupieńczą cechę bycia najprostszą liczbą surrealistyczną w swojej klasie archimedesów; odwrotnie, każda klasa archimedesa w liczbach surrealistycznych zawiera unikalny, najprostszy członek. Tak więc dla każdej dodatniej liczby surrealistycznej x zawsze będzie istniała jakaś dodatnia liczba rzeczywista r i jakaś liczba surrealistyczna y tak, że x − r ω ^y jest „nieskończenie mniejsze” niż x . Wykładnik y jest „logarytmem podstawy ” x , zdefiniowanym na dodatnich surrealach; można wykazać, że log _ω odwzorowuje dodatnie surreale na surreale i że log _ω ( xy ) = log _ω ( x ) + log _ω ( y ).

Jest to rozszerzane przez indukcję pozaskończoną, tak że każda liczba surrealistyczna ma „postać normalną” analogiczną do postaci normalnej Cantora dla liczb porządkowych. To jest postać normalna Conwaya: Każda surrealistyczna liczba x może być jednoznacznie zapisana jako

• x = r ₀ ω ^{Y ₀} + R ₁ ω ^{y ₁} + ...

gdzie każdy r _α jest niezerową liczbą rzeczywistą, a y _α s tworzą ściśle malejący ciąg liczb surrealistycznych. Ta „suma” może jednak mieć nieskończenie wiele wyrazów i ogólnie ma długość dowolnej liczby porządkowej. (Zero odpowiada oczywiście przypadkowi pustego ciągu i jest jedyną liczbą surrealistyczną bez wykładnika wiodącego.)

Patrząc w ten sposób, liczby surrealistyczne przypominają pole szeregu potęgowego , z tym wyjątkiem, że malejące ciągi wykładników muszą być ograniczone na długości przez liczbę porządkową i nie mogą być tak długie jak klasa liczb porządkowych. To jest podstawa do sformułowania liczb surrealistycznych jako szeregu Hahna .

Luki i ciągłość

W przeciwieństwie do liczb rzeczywistych, (właściwy) podzbiór liczb surrealistycznych nie ma najmniejszego ograniczenia górnego (lub dolnego), chyba że ma element maksymalny (minimalny). Conway definiuje lukę jako { L | R }, L < R , L ∪ R = 𝐍𝐨; to nie jest liczba, bo przynajmniej jedna ze stron jest odpowiednią klasą. Choć podobne luki nie są zupełnie takie same jak sekcjach DEDEKIND , ale nadal możemy mówić o zakończeniu 𝐍𝐨 ^𝕯 z surrealistycznych numerów z naturalnej kolejności, która jest (właściwa klasa wielkości) liniowy kontinuum .

Na przykład nie ma najmniejszej dodatniej nieskończoności surrealistycznej, ale przerwa ∞ = { x : ∃ n ∈ : x < n | x : ∀ n ∈ : x > n } jest większa niż wszystkie liczby rzeczywiste i mniejsza niż wszystkie dodatnie nieskończone surreale, a zatem jest najmniejszą górną granicą liczb rzeczywistych w 𝐍𝐨 ^𝕯 . Podobnie luka 𝐎𝐧 = { 𝐍𝐨 | } jest większe niż wszystkie liczby surrealistyczne. (Jest to ezoteryczna gra słów : W ogólnej konstrukcji liczb porządkowych α „jest” zbiorem liczb porządkowych mniejszych niż α i możemy użyć tej równoważności do zapisania α = { α | } w surrealiach; 𝐎𝐧 oznacza klasę liczb porządkowych , a ponieważ 𝐎𝐧 jest kofinalne w 𝐍𝐨, mamy { 𝐍𝐨 | } = { 𝐎𝐧 | } = 𝐎𝐧 przez rozszerzenie). ${\ Displaystyle \ mathbb {N}}$${\ Displaystyle \ mathbb {N}}$

Przy odrobinie staranności w zakresie teorii mnogości 𝐍𝐨 można wyposażyć w topologię, w której zbiory otwarte są sumami przedziałów otwartych (indeksowanych przez odpowiednie zbiory) i można definiować funkcje ciągłe. Można również zdefiniować odpowiednik sekwencji Cauchy'ego, chociaż muszą one być indeksowane przez klasę liczb porządkowych; są zawsze zbieżne, ale granica może być liczbą lub szczelina, która może być wyrażona jako Σ _{α∈𝐍𝐨} R _α Ohm ^_α z _α maleje i mającą dolna granica w 𝐍𝐨. (Wszystkie takie przerwy mogą być rozumiane jako same sekwencje Cauchy'ego, ale istnieją inne typy przerw, które nie są granicami, takie jak ∞ i 𝐎𝐧).

Funkcja wykładnicza

Opierając się na niepublikowanej pracy Kruskala , Gonshor przeprowadził konstrukcję (poprzez indukcję pozaskończoną), która rozszerza rzeczywistą funkcję wykładniczą exp( x ) (o podstawie e ) na surreale.

Inne wykładniki

Te uprawnienia Ohm funkcją jest również funkcja wykładnicza, ale nie mają właściwości pożądane dla rozszerzenia funkcji na liczb rzeczywistych. Będzie to jednak konieczne do rozwoju z Base- e wykładniczy, a jest to funkcja, która jest przeznaczona, gdy oznaczenie ω ^x jest stosowany w dalszym ciągu.

Gdy y jest ułamkiem dwójkowym, funkcja potęgowa x No , x ↦ x ^y może składać się z mnożenia, odwrotności mnożenia i pierwiastka kwadratowego, z których wszystkie można zdefiniować indukcyjnie. Jego wartości są całkowicie określone przez podstawową relację x ^y+z = x ^y ·x ^z , a tam , gdzie jest zdefiniowana, koniecznie zgadza się z każdą inną potęgą, która może istnieć.

Indukcja podstawowa

Kroki indukcyjne dla surrealistycznego wykładnika opierają się na rozwinięciu szeregu dla rzeczywistego wykładniczego, exp x = Σ _{n ≥ 0} x ⁿ /n!, a dokładniej na tych sumach częściowych, które mogą być wykazane przez podstawową algebrę jako dodatnie, ale mniejsze niż wszystkie późniejszych. Dla x dodatnich są one oznaczone [ x ] _n i obejmują wszystkie sumy częściowe; dla x ujemnego, ale skończonego, [ x ] _{2 n +1} oznacza nieparzyste kroki w szeregu zaczynając od pierwszego z dodatnią częścią rzeczywistą (która zawsze istnieje). Dla x ujemnej nieskończoności sumy częściowe nieparzyste są ściśle malejące i notacja [ x ] _{2 n +1} oznacza zbiór pusty, ale okazuje się, że odpowiadające im elementy nie są potrzebne w indukcji.

Relacje, które zachodzą dla rzeczywistego x < y, to exp x · [ y–x ] _n < exp y i exp y · [ x–y ] _{2 n +1} < exp x , co można rozszerzyć na definicja exp z = { 0, exp z _L · [ z–z _L ] _n , exp z _R · [ z–z _R ] _{2 n +1} | exp z _R / [ z _R –z ] _n , exp z _L / [ z _L –z ] _{2 n +1} }. Jest to dobrze zdefiniowane dla wszystkich surrealistycznych argumentów (wartość istnieje i nie zależy od wyboru z _L i z _R ).

Wyniki

Stosując tę ​​definicję, obowiązuje:

• exp jest ściśle rosnącą funkcją dodatnią, x < y ⇒ 0 < exp x < exp y
• exp spełnia exp( x + y ) = exp x · exp y
• exp jest surjekcją (na No ₊ ) i ma dobrze określoną odwrotność, log = exp ^–1
• exp pokrywa się ze zwykłą funkcją wykładniczą na liczbach rzeczywistych (a zatem exp 0 = 1, exp 1 = e )
• Dla x nieskończenie małe, wartość formalnego szeregu potęgowego Σ _{n ≥0} x ⁿ / n ! jest dobrze zdefiniowany i pokrywa się z definicją indukcyjną
  • Gdy x jest podane w postaci normalnej Conwaya, zbiór wykładników w wyniku jest uporządkowany, a współczynniki są sumami skończonymi, bezpośrednio podającymi postać normalną wyniku (który ma wiodący 1)
  • Podobnie, dla x nieskończenie bliskiego 1, log x jest podany przez rozwinięcie szeregu potęgowego x –1
• Dla dodatniej nieskończoności x , exp x również jest nieskończony
  • Jeśli x ma postać ω ^α (α > 0), exp x ma postać ω ^{ω β,} gdzie β jest ściśle rosnącą funkcją α. W rzeczywistości istnieje zdefiniowana indukcyjnie bijekcja g : Nie ₊ → Nie : α ↦ β, której odwrotność można również zdefiniować indukcyjnie
  • Jeśli x jest "czystą nieskończoną" postacią normalną x = Σ _α<β r _α ω ^{a _α} gdzie wszystkie a _α > 0 , wtedy exp x = ω ^{Σ _α<β r _α ω g ( a _α )}
  • Podobnie, dla x = ω ^{Σ _α<β r _α ω b _α} , odwrotność jest dana przez log x = Σ _α<β r _α ω ^{g –1 (b _α )}
• Każda liczba surrealistyczna może być zapisana jako suma czystej nieskończoności, rzeczywistej i nieskończenie małej części, a wykładnicza jest iloczynem wyników cząstkowych podanych powyżej
  • Postać normalną można zapisać, mnożąc część nieskończoną (pojedynczą potęgę ω) i wykładniczą liczbę rzeczywistą w szereg potęgowy wynikający z nieskończenie małej
  • Odwrotnie, wydzielenie wyrazu wiodącego postaci normalnej przyniesie dowolną liczbę surrealistyczną do postaci (ω ^{Σ _γ<δ t _γ ω b _γ} )· r ·(1 + Σ _α<β s _α ω ^{a _α} ) , dla a _α < 0 , gdzie każdy czynnik ma postać, dla której sposób obliczenia logarytmu podano powyżej; suma jest wtedy logarytmem ogólnym
    • Chociaż nie ma ogólnej indukcyjnej definicji log (w przeciwieństwie do exp), wyniki cząstkowe są podawane w terminach takich definicji. W ten sposób logarytm można obliczyć wprost, bez odniesienia do faktu, że jest odwrotnością wykładnika.
• Funkcja wykładnicza jest znacznie większa niż jakakolwiek skończona potęga
  • Dla dowolnej dodatniej nieskończonej x i dowolnego skończonego n exp( x )/ x ⁿ jest nieskończone
  • Dla dowolnej liczby całkowitej n i surrealistycznej x > n ² , exp( x ) > x ⁿ . To silniejsze ograniczenie jest jednym z aksjomatów Ressayre'a dla rzeczywistego pola wykładniczego
• exp spełnia wszystkie aksjomaty Ressayre'a dla rzeczywistego pola wykładniczego
  • Surrealistyczne z wykładnikiem jest elementarnym rozszerzeniem rzeczywistego pola wykładniczego
  • Dla ε _β liczby porządkowej epsilon, zbiór liczb surrealistycznych z datą urodzenia mniejszą niż ε _β stanowi pole, które jest domknięte pod wykładnikami i jest również elementarnym rozszerzeniem rzeczywistego pola wykładniczego

Przykłady

Surrealistyczny wykładnik jest zasadniczo dany przez jego zachowanie na dodatnich potęgach ω, tj. funkcji g(a) , w połączeniu z dobrze znanym zachowaniem na liczbach skończonych. Podane zostaną tylko przykłady tych pierwszych. Ponadto g(a) = a obowiązuje dla dużej części jego zakresu, na przykład dla dowolnej liczby skończonej z dodatnią częścią rzeczywistą i dowolnej liczby nieskończonej mniejszej niż pewna iterowana potęga ω ( ω ^{ω · · ω} dla pewnej liczby poziomów).

• exp ω = ω ^ω
• exp ω ^1/ω = ω i log ω = ω ^1/ω
• exp (ω · log ω) = exp (ω · ω ^1/ω ) = ω ^{ω (1 + 1/ω)}
  • To pokazuje, że funkcja „Power of Ohm” nie jest kompatybilny z exp, ponieważ zgodności wymagałoby wartość Ohm ^Ohm tutaj
• exp ε ₀ = ω ^{ω ε ₀ + 1}
• log ε ₀ = ε ₀ / ω

Potęgowanie

Ogólne potęgowanie można zdefiniować jako x ^y = exp( y · log x ) , dając interpretację wyrażeniom takim jak 2 ^ω = exp(ω · log 2) = ω ^{log 2 · ω} . Ponownie, konieczne jest odróżnienie tej definicji od funkcji „potęg ω”, zwłaszcza jeśli ω może występować jako podstawa.

Liczby nadkompleksowe

Liczba surcomplex szereg postaci + b I , gdzie i b są liczbami surrealistyczne i i jest pierwiastkiem kwadratowym z -1 . Numery surcomplex tworzą algebraicznie zamknięte pole (z wyjątkiem jest odpowiednia klasa), izomorficzne z algebraicznej zamknięcie pola wytwarzanego przez rozszerzenie liczby wymierne przez odpowiedniej klasie z algebraicznie niezależnych transcendentalnych elementów. Aż do izomorfizmu pól , fakt ten charakteryzuje pole liczb nadkompleksowych w ramach dowolnej teorii zbiorów ustalonych.

Gry

Definicja liczb surrealistycznych zawierała jedno ograniczenie: każdy element L musi być ściśle mniejszy niż każdy element R. Jeśli to ograniczenie zostanie usunięte, możemy wygenerować bardziej ogólną klasę znaną jako gry . Wszystkie gry są konstruowane zgodnie z tą zasadą:

Reguła konstrukcji
Jeśli L i R są dwoma zestawami gier, to { L | R } to gra.

Dodawanie, negacja i porównanie są definiowane w ten sam sposób zarówno dla liczb surrealistycznych, jak i gier.

Każda liczba surrealistyczna jest grą, ale nie wszystkie gry są liczbami surrealistycznymi, np. gra { 0 | 0 } nie jest liczbą surrealistyczną. Klasa gier jest bardziej ogólna niż surrealistyczne i ma prostszą definicję, ale brakuje jej niektórych ładniejszych właściwości liczb surrealistycznych. Klasa liczb surrealistycznych tworzy pole , ale klasa gier nie. Surreale mają całkowity porządek : biorąc pod uwagę dowolne dwie surreale, są one albo równe, albo jedna jest większa od drugiej. Gry mają tylko częściowy porządek : istnieją pary gier, które nie są ani równe, ani większe, ani mniejsze od siebie. Każda liczba surrealistyczna jest dodatnia, ujemna lub zero. Każda gra jest albo dodatnia, ujemna, zerowa , albo rozmyta (nieporównywalna z zerem, np. {1|−1}).

Ruch w grze polega na tym, że gracz, którego ruchem wybiera grę spośród dostępnych w L (dla lewego gracza) lub R (dla prawego gracza), a następnie przekazuje wybraną grę innemu graczowi. Gracz, który nie może się poruszyć, ponieważ wybór pochodzi z pustego zestawu, przegrał. Pozytywna gra oznacza wygraną dla lewego gracza, negatywną grę dla prawego gracza, zerową grę dla drugiego gracza i rozmytą grę dla pierwszego gracza.

Jeśli x , y i z są surrealiami, a x = y , to x z = y z . Jeśli jednak x , y i z są grami, a x = y , to nie zawsze jest prawdą, że x z = y z . Zauważ, że „=” oznacza tutaj równość, a nie tożsamość.

Zastosowanie do kombinatorycznej teorii gier

Liczby surrealistyczne były pierwotnie motywowane studiami nad grą Go i istnieje wiele powiązań między popularnymi grami a surrealizmami. W tej sekcji użyjemy Game pisanej wielkimi literami dla obiektu matematycznego {L|R}, a gry pisanej małymi literami dla gier rekreacyjnych, takich jak Szachy lub Go .

Rozważamy gry o tych właściwościach:

• Dwóch graczy (o nazwie Lewy i Prawy )
• Deterministyczny (gra na każdym etapie będzie całkowicie zależeć od wyborów dokonywanych przez graczy, a nie od czynnika losowego)
• Brak ukrytych informacji (takich jak karty lub płytki, które gracz ukrywa)
• Gracze naprzemiennie wykonują tury (gra może, ale nie musi zezwalać na wielokrotne ruchy w turze)
• Każda gra musi kończyć się skończoną liczbą ruchów
• Gdy nie ma już żadnych dozwolonych ruchów dla gracza, gra się kończy, a gracz przegrywa

W większości gier początkowa pozycja na planszy nie daje żadnej przewagi żadnemu z graczy. W miarę postępów gry i gdy jeden gracz zaczyna wygrywać, pojawią się pozycje na planszy, na których ten gracz ma wyraźną przewagę. Do analizy gier przydatne jest skojarzenie gry z każdą pozycją planszy. Wartością danej pozycji będzie Gra {L|R}, gdzie L jest zbiorem wartości wszystkich pozycji, które można osiągnąć jednym ruchem Lewym. Podobnie, R jest zbiorem wartości wszystkich pozycji, które można osiągnąć jednym ruchem w prawo.

Gra zero (zwana 0) to Gra, w której L i R są puste, więc gracz, który przejdzie dalej (L lub R) natychmiast przegrywa. Suma dwóch Gier G = { L1 | R1 } i H = { L2 | R2 } jest zdefiniowany jako Gra G + H = { L1 + H, G + L2 | R1 + H, G + R2 }, gdzie gracz, który ma się poruszyć, wybiera, w którą z gier będzie grać na każdym etapie, a przegrany nadal pozostaje graczem, który nie wykona żadnego ruchu. Można sobie wyobrazić dwie szachownice między dwoma graczami, z graczami wykonującymi ruchy naprzemiennie, ale z całkowitą swobodą, na której planszy grać. Jeśli G jest grą {L | R}, -G to gra {-R | -L}, czyli z odwróconą rolą dwóch graczy. Łatwo jest pokazać G - G = 0 dla wszystkich Gier G (gdzie G - H jest zdefiniowane jako G + (-H)).

Ten prosty sposób kojarzenia gier z grami daje bardzo ciekawy wynik. Załóżmy, że dwóch doskonałych graczy gra w grę, zaczynając od podanej pozycji, której powiązana jest Gra x . Wszystkie gry możemy podzielić na cztery klasy w następujący sposób:

• Jeśli x > 0, Lewy wygra, niezależnie od tego, kto zagra pierwszy.
• Jeśli x < 0, wygra prawa, niezależnie od tego, kto zagra pierwszy.
• Jeśli x = 0, wygra gracz, który zajmie drugie miejsce.
• Jeśli x || 0, wygra gracz, który pójdzie pierwszy.

Bardziej ogólnie, możemy zdefiniować G > H jako G - H > 0 i podobnie dla <, = i ||.

Oznaczenie G || H oznacza, że ​​G i H są nieporównywalne. G || H jest równoważne G−H || 0, tzn. że G > H, G < H i G = H są fałszywe. Czasami mówi się, że nieporównywalne gry są ze sobą mylone , ponieważ jedna lub druga może być preferowana przez gracza w zależności od tego, co do niego doda. Mówi się, że gra pomylona z zerem jest rozmyta , w przeciwieństwie do dodatniej, ujemnej lub zerowej . Przykładem gry rozmytej jest gwiazdka (*) .

Czasami, gdy gra zbliża się do końca, rozpada się na kilka mniejszych gier, które nie wchodzą w interakcje, z wyjątkiem tego, że tura każdego gracza pozwala na poruszanie się tylko w jednej z nich. Na przykład w Go plansza będzie powoli zapełniać się pionkami, aż będzie tylko kilka małych wysp pustej przestrzeni, na których gracz może się poruszać. Każda wyspa jest jak osobna gra w Go, rozgrywana na bardzo małej planszy. Przydałoby się, gdyby każdą podgrę można było analizować osobno, a następnie połączyć wyniki, aby uzyskać analizę całej gry. Nie wydaje się to łatwe. Na przykład mogą istnieć dwie podgry, w których kto pierwszy wykona ruch, wygrywa, ale gdy zostaną one połączone w jedną wielką grę, nie wygrywa już pierwszy gracz. Na szczęście istnieje sposób na wykonanie tej analizy. Można zastosować następujące twierdzenie:

Jeśli duża gra rozkłada się na dwie mniejsze, a małe gry mają powiązaną Grę x i y , to duża gra będzie miała powiązaną Grę x + y .

Gra złożona z mniejszych gier nazywana jest rozłączną sumą tych mniejszych gier, a twierdzenie mówi, że zdefiniowana przez nas metoda dodawania jest równoważna wzięciu rozłącznej sumy dodatków.

Historycznie Conway rozwinął teorię liczb surrealistycznych w odwrotnej kolejności niż została tutaj przedstawiona. Analizował gry końcowe w Go i zdał sobie sprawę, że przydałby się jakiś sposób na połączenie analiz nieoddziałujących podgier w analizę ich sumy rozłącznej . Na tej podstawie wymyślił koncepcję Gry i operatora dodawania do niej. Następnie przeszedł do opracowania definicji negacji i porównania. Potem zauważył, że pewna klasa gier ma interesujące właściwości; ta klasa stała się liczbami surrealistycznymi. W końcu opracował operator mnożenia i dowiódł, że surreali są w rzeczywistości polem, które obejmuje zarówno liczby rzeczywiste, jak i porządkowe.

Alternatywne realizacje

Alternatywne podejścia do surrealistycznych liczb uzupełniają ekspozycję Conwaya w zakresie gier.

Rozszerzenie znaku

Definicje

W tym, co teraz nazywamy rozszerzeniem znaku lub ciągiem znaków liczby surrealistycznej, liczba surrealistyczna jest funkcją, której dziedzina jest porządkowa i której przeciwdziedziną jest {-1, +1 }. Jest to odpowiednik sekwencji LR Conwaya.

Określić orzeczenie binarne "prostsze niż" na liczby, x jest prostsza niż Y , gdy x jest podzbiorem z Y , to znaczy , gdy dom ( x ) <dom ( y ) i x (α) = Y (α) dla wszystkich alfa < dom( x ).

Dla liczb surrealistycznych definiuj relację binarną < jako porządek leksykograficzny (z konwencją, że „niezdefiniowane wartości” są większe niż -1 i mniejsze niż 1). Więc x < y, jeśli zachodzi jedno z poniższych:

• x jest prostsze niż y i y (dom( x )) = + 1;
• y jest prostsze niż x i x (dom( y )) = − 1;
• istnieje liczba z taka, że z jest prostsze niż x , z jest prostsze niż y , x (dom( z )) = − 1 i y (dom( z )) = + 1.

Równoważnie, niech δ( x , y ) = min({ dom( x ), dom( y )} ∪ { α : α < dom( x ) ∧ α < dom( y ) ∧ x (α) ≠ y (α) }), więc x = y wtedy i tylko wtedy, gdy δ( x , y ) = dom( x ) = dom( y ). Wtedy, dla liczb x i y , x < y wtedy i tylko wtedy, gdy zachodzi jedno z poniższych:

• δ( x , y ) = dom( x ) ∧ δ( x , y ) < dom( y ) ∧ y (δ( x , y )) = + 1;
• δ( x , y ) < dom( x ) ∧ δ( x , y ) = dom( y ) ∧ x (δ( x , y )) = − 1;
• δ( x , y ) < dom( x ) ∧ δ( x , y ) < dom( y ) ∧ x (δ( x , y )) = − 1 ∧ y (δ( x , y )) = + 1.

Dla liczb x i y , x ≤ y wtedy i tylko wtedy, gdy x < y ∨ x = y , a x > y wtedy i tylko wtedy, gdy y < x . Również x ≥ y wtedy i tylko wtedy, gdy y ≤ x .

Relacja <jest przechodni , a dla wszystkich liczb x i y dokładnie jeden z x < y , x = y , x > y , posiada (ustawa z trichotomię ). Oznacza to, że < jest porządkiem liniowym (poza tym, że < jest właściwą klasą).

Dla zbiorów liczb L i R takich, że ∀ x ∈ L ∀ y ∈ R ( x < y ), istnieje jednoznaczna liczba z taka, że

• ∀ x ∈ L ( x < z ) ∧ ∀ y ∈ R ( z < y ),
• Dla dowolnej liczby w takiej, że ∀ x ∈ L ( x < w ) ∧ ∀ y ∈ R ( w < y ), w = z lub z jest prostsze niż w .

Ponadto z można skonstruować z L i R przez indukcję pozaskończoną. z jest najprostszą liczbą pomiędzy L i R . Niech unikalna liczba z będzie oznaczona przez σ( L , R ).

Dla liczby x zdefiniuj jej lewy zbiór L ( x ) i prawy zbiór R ( x ) przez

• L ( x ) = { x | _α  : α < dom( x ) ∧ x (α) = + 1 };
• R ( x ) = { x | _α  : α < dom( x ) ∧ x (α) = − 1 },

wtedy σ( L ( x ), R ( x )) = x .

Jedną z zalet tej alternatywnej realizacji jest to, że równość jest tożsamością, a nie indukcyjnie zdefiniowaną relacją. Jednak w przeciwieństwie do realizacji Conwaya o liczbach surrealistycznych, rozszerzenie znaku wymaga wcześniejszej konstrukcji liczb porządkowych, podczas gdy w realizacji Conwaya liczby porządkowe są konstruowane jako szczególne przypadki surrealiów.

Można jednak poczynić podobne definicje, które eliminują potrzebę wcześniejszego konstruowania liczb porządkowych. Na przykład, moglibyśmy pozwolić, aby surreale były (rekurencyjnie definiowaną) klasą funkcji, których dziedzina jest podzbiorem surreali spełniających regułę przechodniości ∀ g ∈ dom f (∀ h ∈ dom g ( h ∈ dom f )) i których zakres to { −, + }. „Prostsze niż” jest teraz bardzo prosto zdefiniowane — x jest prostsze niż y, jeśli x ∈ dom y . Całkowite uporządkowanie jest definiowane przez rozważenie x i y jako zbiorów uporządkowanych par (jak zwykle definiuje się funkcję): albo x = y , albo liczba surrealistyczna z = x ∩ y jest w domenie x lub w domenie y (lub oba, ale w tym przypadku znaki muszą się nie zgadzać). Mamy wtedy x < y, jeśli x ( z ) = − lub y ( z ) = + (lub oba). Przekształcenie tych funkcji w sekwencje znaków jest prostym zadaniem; ułóż elementy dom f w kolejności prostoty (tj. inkluzji), a następnie zapisz kolejno znaki, które f przypisuje każdemu z tych elementów. Liczby porządkowe występują wtedy naturalnie jako te liczby surrealistyczne, których zakres wynosi { + }.

Dodawanie i mnożenie

Suma x + y dwóch liczb, x i y , jest określona przez indukcję na dom( x ) i dom( y ) przez x + y = σ( L , R ), gdzie

• L = { u + y  : u ∈ L ( x ) } ∪ { x + v  : v ∈ L ( y ) },
• R = { u + y  : u ∈ R ( x ) } ∪ { x + v  : v ∈ R ( y ) }.

Tożsamość addytywna jest dana przez liczbę 0 = { }, tzn . liczba 0 jest unikalną funkcją, której dziedziną jest liczba porządkowa 0, a addytywna odwrotność liczby x to liczba − x , podana przez dom(− x ) = dom( x ), oraz, dla α < dom( x ), (− x )(α) = − 1 jeśli x (α) = + 1, oraz (− x )(α) = + 1 jeśli x (α) = − 1.

Wynika z tego, że liczba x jest dodatnia wtedy i tylko wtedy, gdy 0 < dom( x ) i x (0) = + 1, a x jest ujemne wtedy i tylko wtedy, gdy 0 < dom( x ) i x (0) = − 1.

Iloczyn xy dwóch liczb, x i y , jest określony przez indukcję na dom( x ) i dom( y ) przez xy = σ( L , R ), gdzie

• L = { uy + xv − uv  : u ∈ L ( x ), v ∈ L ( y ) } ∪ { uy + xv − uv  : u ∈ R ( x ), v ∈ R ( y ) },
• R = { uy + xv − uv  : u ∈ L ( x ), v ∈ R ( y ) } ∪ { uy + xv − uv  : u ∈ R ( x ), v ∈ L ( y ) }.

Tożsamość multiplikatywna jest dana przez liczbę 1 = { (0,+1) }, tzn . liczba 1 ma dziedzinę równą liczbie porządkowej 1, a 1(0) = + 1.

Korespondencja z realizacją Conwaya

Mapa z realizacji Conwaya do rozwinięć ze znakiem jest dana wzorem f ({ L | R }) = σ( M , S ), gdzie M = { f ( x ) : x ∈ L } i S = { f ( x ) : x ∈ R }.

Odwrotność odwzorowania z realizacji alternatywnej do realizacji Conwaya jest dana przez g ( x ) = { L | R } , gdzie L = { g ( y ) : y ∈ L ( x ) } i R = { g ( y ) : y ∈ R ( x ) }.

Podejście aksjomatyczne

W innym podejściu do surrealiów, podanym przez Allinga, wyraźna konstrukcja zostaje całkowicie pominięta. Zamiast tego podany jest zestaw aksjomatów, które musi spełniać każde konkretne podejście do surrealiów. Podobnie jak aksjomatyczne podejście do rzeczywistości, te aksjomaty gwarantują unikalność aż do izomorfizmu.

Trójka to surrealistyczny system liczbowy wtedy i tylko wtedy, gdy spełniony jest następujący warunek: ${\ Displaystyle \ langle \ mathbf {nie}, \ operatorname {<}, b \ rangle}$

• < to całkowite zamówienie ponad Nie
• b jest funkcją z No na klasę wszystkich liczb porządkowych ( b jest nazywana „funkcją urodzin” w No ).
• Niech A i B będą podzbiorami No takimi, że dla wszystkich x ∈ A i y ∈ B , x < y (używając terminologii Allinga, 〈A , B〉 jest "cięciem Conwaya" z No ). Wtedy istnieje jednoznaczne z ∈ No takie, że b(z) jest minimalne i dla wszystkich x ∈ A i wszystkich y ∈ B , x < z < y . (Ten aksjomat jest często określany jako „Twierdzenie o prostocie Conwaya”).
• Ponadto, jeśli liczba porządkowa α jest większa niż b(x) dla wszystkich x ∈ A , B , wtedy b(z) ≤ α . (Alling nazywa system, który spełnia ten aksjomat, „w pełni surrealistycznym systemem liczbowym”).

Zarówno oryginalna konstrukcja Conwaya, jak i konstrukcja ekspansji znaku surrealów spełniają te aksjomaty.

Biorąc pod uwagę te aksjomaty, Alling wyprowadza oryginalną definicję ≤ Conwaya i rozwija arytmetykę surrealistyczną.

Hierarchia prostoty

Konstrukcję liczb surrealistycznych jako maksymalnego binarnego pseudodrzewa z prostotą (przodkiem) i uporządkowaniem relacji zawdzięczamy Philipowi Ehrlichowi. Różnica od zwykłej definicji drzewa polega na tym, że zbiór przodków wierzchołka jest uporządkowany, ale nie może mieć elementu maksymalnego (bezpośredni poprzednik); innymi słowy, typ porządku tego zbioru to ogólna liczba porządkowa, a nie tylko liczba naturalna. Ta konstrukcja spełnia również aksjomaty Allinga i może być łatwo odwzorowana na reprezentację ciągu znakowego.

Seria Hahna

Alling udowadnia również, że ciało liczb surrealistycznych jest izomorficzne (jako ciało uporządkowane) z ciałem szeregu Hahna o współczynnikach rzeczywistych na grupie wartości samych liczb surrealistycznych (reprezentacja szeregu odpowiadająca postaci normalnej liczby surrealistycznej, zgodnie z definicją nad). Zapewnia to związek między liczbami surrealistycznymi a bardziej konwencjonalnymi podejściami matematycznymi do uporządkowanej teorii pola.

Ten izomorfizm przekształca liczby surrealistyczne w pole wartościowe, gdzie wartościowanie jest addytywną odwrotnością wykładnika wyrazu wiodącego w postaci normalnej Conwaya, np. ν(ω) = -1. Pierścień wartościujący składa się wtedy ze skończonych liczb surrealistycznych (liczby z częścią rzeczywistą i/lub nieskończenie małą). Powodem odwrócenia znaku jest to, że wykładniki w postaci normalnej Conwaya stanowią dobrze uporządkowany zbiór odwrotny, podczas gdy szeregi Hahna są sformułowane w kategoriach (nieodwróconych) dobrze uporządkowanych podzbiorów grupy wartości.

Relacja z hiperrealami

Philip Ehrlich skonstruował izomorfizm między maksymalnym nadrzeczywistym ciałem liczbowym Conwaya a maksymalnymi hiperrzeczywistymi w teorii mnogości von Neumanna-Bernaysa-Gödla .

Zobacz też

• Liczba hiperrzeczywista
• Analiza niestandardowa

Uwagi

Bibliografia

Dalsza lektura

• Oryginalna ekspozycja Donalda Knutha : Surreal Numbers: How Two Ex-Students Turned to Pure Mathematics and Found Total Happiness , 1974, ISBN  0-201-03812-9 . Więcej informacji można znaleźć na oficjalnej stronie internetowej książki .
• Aktualizacja klasycznej książki z 1976 roku definiującej liczby surrealistyczne i badającej ich powiązania z grami: John Conway, On Numbers And Games , wyd. 2, 2001, ISBN  1-56881-127-6 .
• Aktualizacja pierwszej części książki z 1981 r., która przedstawiała szerszej publiczności liczby surrealistyczne i analizę gier: Berlekamp, ​​Conway i Guy, Winning Ways for Your Mathematical Plays , t. 1, wyd. 2, 2001, ISBN  1-56881-130-6 .
• Martin Gardner , Penrose Tiles to Trapdoor Ciphers, WH Freeman & Co., 1989, ISBN  0-7167-1987-8 , rozdział 4. Przegląd nietechniczny; przedruk artykułu Scientific American z 1976 roku.
• Polly Shulman, "Infinity Plus One, and Other Surreal Numbers" , Discover , grudzień 1995.
• Szczegółowa analiza liczb surrealistycznych: Norman L. Alling, Foundations of Analysis over Surreal Number Fields , 1987, ISBN  0-444-70226-1 .
• Traktowanie surrealiów oparte na realizacji ekspansji znakowej: Harry Gonshor, Wprowadzenie do teorii liczb surrealistycznych , 1986, ISBN  0-521-31205-1 .
• Szczegółowy rozwój filozoficzny pojęcia liczb surrealistycznych jako najbardziej ogólnego pojęcia liczby: Alain Badiou , Number and Numbers , New York: Polity Press, 2008, ISBN  0-7456-3879-1 (miękka oprawa ), ISBN  0-7456- 3878-3 (twarda okładka).
• Program Fundacji Uniwalentnych (2013). Teoria typów homotopii: jednowartościowe podstawy matematyki . Princeton, NJ: Instytut Studiów Zaawansowanych . MR  3204653 .Liczby surrealistyczne są badane w kontekście teorii typu homotopii w sekcji 11.6.

Zewnętrzne linki

• Hackenstrings i 0.999... ?= 1 FAQ, AN Walker , archiwum zaginionego oryginału
• Delikatne, ale dokładne wprowadzenie Clausa Tøndering
• Good Math, Bad Math: Surreal Numbers , seria artykułów o liczbach surrealistycznych i ich odmianach