Zestaw Cantora - Cantor set

W matematyce , zbiór Cantora jest zbiór punktów leżących na jednym odcinku linii , który ma szereg właściwości nieintuicyjne. Został odkryty w 1874 roku przez Henry'ego Johna Stephena Smitha i wprowadzony przez niemieckiego matematyka Georga Cantora w 1883 roku.

Rozważając ten zbiór, Cantor i inni pomogli położyć podwaliny pod nowoczesną topologię zbioru punktów . Chociaż sam Cantor zdefiniował zbiór w sposób ogólny, abstrakcyjny, najpowszechniejszą współczesną konstrukcją jest zbiór trójkowy Cantora , budowany przez usunięcie środkowej trzeciej części odcinka, a następnie powtórzenie procesu z pozostałymi krótszymi odcinkami. Sam Cantor tylko mimochodem wspomniał o konstrukcji trójskładnikowej, jako przykładu ogólniejszej idei, czyli zbioru doskonałego, który nigdzie nie jest gęsty .

Powiększ zestaw Cantora. Każdy punkt w zbiorze jest tutaj reprezentowany przez pionową linię.

Budowa i formuła zbioru trójskładnikowego

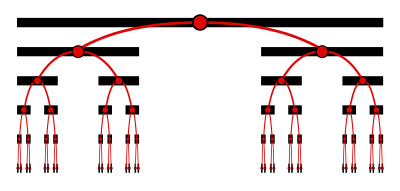
Trójskładnikowy zbiór Cantora jest tworzony przez iteracyjne usuwanie otwartej tercji środkowej ze zbioru odcinków linii. Rozpoczyna się od usunięcia otwartej tercji środkowej z przedziału , pozostawiając dwa odcinki linii: . Następnie otwarta środkowa jedna trzecia każdego z pozostałych segmentów jest usuwana, pozostawiając cztery segmenty linii: . Ten proces jest kontynuowany w nieskończoność , gdzie n- ty zbiór to ${\displaystyle {\mathcal {C}}}$${\textstyle \left({\frac {1}{3}},{\frac {2}{3}}\right)}$ ${\ Displaystyle \ textstyle \ lewo [0, 1 \ prawo]}$${\textstyle \left[0,{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},1\right]}$${\textstyle \left[0,{\frac {1}{9}}\right]\cup \left[{\frac {2}{9}},{\frac {1}{3}}\right] \cup \left[{\frac {2}{3}},{\frac {7}{9}}\right]\cup \left[{\frac {8}{9}},1\right]}$

${\ Displaystyle C_ {n} = {\ Frac {C_ {C_ {n-1}} {3}} \ filiżanka \ lewo ({\ Frac {2} {3}} + {\ Frac {C_ {n-1}}} {3}}\right){\text{ dla }}n\geq 1,{\text{ i }}C_{0}=[0,1].}$

Trójskładnikowy zbiór Cantora zawiera wszystkie punkty w przedziale , które nie są usuwane na żadnym etapie tego nieskończonego procesu: ${\displaystyle [0,1]}$

${\ Displaystyle {\ mathcal {C}}: = \ bigcap _ {n = 0} ^ {\ infty} C_ {n} = \ bigcap _ {n = m} ^ {\ infty} C_ {n}}$   dla każdego   ${\displaystyle m\geq 0.}$

Poniżej zilustrowano pierwszych sześć kroków tego procesu.

Wykorzystując ideę przekształceń samopodobnych i jawnie zamknięte formuły dla zbioru Cantora są: ${\ Displaystyle T_ {L} (x) = x / 3 T_ {R} (x) = (2 + x) / 3}$${\ Displaystyle C_ {n} = T_ {L} (C_ {n-1}) \ filiżanka T_ {R} (C_ {n-1})}$

${\ Displaystyle {\ mathcal {C}} = [0,1] \ \ setminus \ \ bigcup _ {n = 0} ^ {\ infty} \ bigcup _ {k = 0} ^ {3 ^ {n} -1}\lewo({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\prawo),}$

gdzie każda środkowa trzecia jest usuwana jako przedział otwarty z otaczającego go przedziału zamkniętego , lub ${\textstyle \left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)}$${\textstyle \left[{\frac {3k+0}{3^{n+1}}},{\frac {3k+3}{3^{n+1}}}\right]=\left[ {\frac {k+0}{3^{n}}},{\frac {k+1}{3^{n}}}\prawo]}$

${\ Displaystyle {\ mathcal {C}} = \ bigcap _ {n = 1} ^ {\ infty} \ bigcup _ {k = 0} ^ {3 ^ {n-1} -1} \ lewo (\ lewo [ {\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{ 3^{n}}},{\frac {3k+3}{3^{n}}}\w prawo]\w prawo),}$

gdzie środkowa jedna trzecia powyższego zamkniętego przedziału jest usuwana przez przecięcie z${\textstyle \left({\frac {3k+1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)}$${\textstyle \left[{\frac {k+0}{3^{n-1}}},{\frac {k+1}{3^{n-1}}}\right]=\left[ {\frac {3k+0}{3^{n}}},{\frac {3k+3}{3^{n}}}\prawo]}$${\textstyle \left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\prawo].}$

Ten proces usuwania środkowych trzecich jest prostym przykładem reguły skończonego podziału . Trójskładnikowy zbiór Cantora jest przykładem łańcucha fraktalnego .

W kategoriach arytmetycznych zbiór Cantora składa się ze wszystkich liczb rzeczywistych przedziału jednostkowego , które nie wymagają cyfry 1, aby były wyrażone jako ułamek trójkowy (o podstawie 3). Jak ilustruje powyższy diagram, każdy punkt w zbiorze Cantora jest unikalnie zlokalizowany przy ścieżce przez nieskończenie głębokie drzewo binarne, gdzie ścieżka skręca w lewo lub w prawo na każdym poziomie, w zależności od tego, po której stronie usuniętego segmentu znajduje się punkt. Reprezentowanie każdego skrętu w lewo przez 0 i każdego skrętu w prawo przez 2 daje ułamek trójkowy dla punktu. ${\displaystyle [0,1]}$

Kompozycja

Ponieważ zbiór Cantora jest zdefiniowany jako zbiór punktów, które nie są wykluczone, proporcję (tj. miarę ) pozostałego przedziału jednostkowego można znaleźć według całkowitej usuniętej długości. Ta suma to postęp geometryczny

${\ Displaystyle \ suma _ {n = 0} ^ {\ infty} {\ Frac {2 ^ {n}} {3 ^ {n + 1}}} = {\ Frac {1} {3}} + {\ frac {2}{9}}+{\frac {4}{27}}+{\frac {8}{81}}+\cdots ={\frac {1}{3}}\po lewej({\frac {1}{1-{\frac {2}{3}}}}\right)=1.}$

Aby pozostała proporcja to 1 − 1 = 0.

Obliczenie to sugeruje, że zbiór Cantora nie może zawierać żadnego przedziału o niezerowej długości. Może wydawać się zaskakujące, że powinno być cokolwiek – w końcu suma długości usuniętych przedziałów jest równa długości przedziału pierwotnego. Jednak bliższe przyjrzenie się temu procesowi pokazuje, że musi coś jeszcze zostać, ponieważ usunięcie „środkowej trzeciej” każdego interwału wymagało usunięcia otwartych zbiorów (zbiorów, które nie zawierają swoich punktów końcowych). Więc usunięcie segmentu linii (1/3, 2/3) z pierwotnego przedziału [0, 1] pozostawia za sobą punkty 1/3 oraz 2/3. Kolejne kroki nie usuwają tych (lub innych) punktów końcowych, ponieważ usunięte przedziały są zawsze wewnętrzne względem pozostałych przedziałów. Tak więc zbiór Cantora nie jest pusty, aw rzeczywistości zawiera nieprzeliczalnie nieskończoną liczbę punktów (jak wynika z powyższego opisu w kategoriach ścieżek w nieskończonym drzewie binarnym).

Może się wydawać, że pozostały tylko końce segmentów konstrukcyjnych, ale tak nie jest. Numer1/4, Na przykład, ma unikalną formę potrójny 0.020202 ... = 0. 02 . Znajduje się w dolnej jednej trzeciej, górnej jednej trzeciej tej trzeciej, dolnej trzeciej górnej trzeciej i tak dalej. Ponieważ nigdy nie znajduje się w jednym ze środkowych segmentów, nigdy nie jest usuwany. Nie jest to jednak również punkt końcowy żadnego środkowego segmentu, ponieważ nie jest wielokrotnością żadnej potęgi 1/3. Wszystkie punkty końcowe segmentów są końcowymi ułamkami trójskładnikowymi i są zawarte w zestawie

${\ Displaystyle \ lewo \ {x \ w [0, 1] \ mid \ istnieje ja \ w \ mathbb {N} _ {0}: x \, 3 ^ {i} \ w \ mathbb {Z} \ prawej \ }\qquad {\Bigl (}\subset \mathbb {N} _{0}\,3^{-\mathbb {N} _{0}}{\Bigr )}}$

który jest przeliczalnie nieskończonym zbiorem. Co do kardynalności , prawie wszystkie elementy zbioru Cantora nie są punktami końcowymi przedziałów, ani punktami wymiernymi jak 1/4. Cały zbiór Cantora jest właściwie niepoliczalny.

Nieruchomości

Kardynalność

Można wykazać, że w tym procesie pozostało tyle punktów, ile było na początku, a zatem zbiór Cantora jest niepoliczalny . Aby to zobaczyć, pokażemy, że istnieje funkcja f ze zbioru Cantora do zamkniętego przedziału [0,1], który jest suriekcją (czyli f map z na [0,1]), tak, że liczność z nie mniej niż z [0,1]. Ponieważ jest podzbiorem [0,1], jego kardynalność również nie jest większa, więc obie moce muszą w rzeczywistości być równe, zgodnie z twierdzeniem Cantora-Bernsteina-Schrödera . ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Aby skonstruować tę funkcję, rozważ punkty w przedziale [0, 1] pod względem notacji o podstawie 3 (lub trójskładnikowej ). Przypomnijmy, że właściwe ułamki trójskładnikowe, a dokładniej: elementy , dopuszczają w tym zapisie więcej niż jedną reprezentację, jak na przykład${\ Displaystyle {\ bigl (} \ mathbb {Z} \ setminus \ {0 \} {\ duży}} \ cdot 3 ^ {- \ mathbb {N} _ {0}}}$1/3, które można zapisać jako 0,1 ₃ = 0,1 0 ₃ , ale także jako 0,0222... ₃ = 0,0 2 ₃ , oraz2/3, który można zapisać jako 0,2 ₃ = 0,2 0 ₃ ale także jako 0,1222... ₃ = 0,1 2 ₃ . Gdy usuniemy środkową tercję, zawiera ona liczby z cyframi trójskładnikowymi w postaci 0.1xxxxx... ₃ gdzie xxxxx... ₃ jest ściśle pomiędzy 00000... ₃ a 22222... ₃ . Tak więc liczby pozostałe po pierwszym kroku składają się z

• Liczby postaci 0.0xxxxx... ₃ (w tym 0.022222... ₃ = 1/3)
• Liczby postaci 0.2xxxxx... ₃ (w tym 0.222222... ₃ = 1)

Można to podsumować mówiąc, że te liczby z reprezentacją trójskładnikową, tak że pierwsza cyfra po punkcie podstawy nie jest 1, są tymi pozostałymi po pierwszym kroku.

Drugi krok usuwa liczby w postaci 0.01xxxx... ₃ i 0.21xxxx... ₃ , i (z należytą dbałością o punkty końcowe) można wywnioskować, że pozostałe liczby to te z liczebnikiem trójczłonowym, gdzie żadna z pierwszych dwie cyfry to 1.

Kontynuując w ten sposób, aby liczba nie była wykluczona w kroku n , musi mieć reprezentację trójskładnikową, której n- ta cyfra nie jest 1. Aby liczba była w zbiorze Cantora, nie może być wykluczona na żadnym kroku, musi dopuszczać reprezentację liczbową składającą się wyłącznie z zer i dwójek.

Warto podkreślić, że liczby takie jak 1, 1/3= 0,1 ₃ i7/90,21 ₃ znajdują się w zbiór Cantora, ponieważ mają cyfry trójskładnikowe składający się w całości z 0s i 2S = 0,222: 1 ... ₃ = 0, 2 ₃ ,1/3= 0,0222... ₃ = 0,0 2 ₃ i7/9= 0,20222... ₃ = 0,20 2 ₃ . Wszystkie te ostatnie numery są „punkty końcowe”, a te przykłady to prawy punkt skupienia z . To samo dotyczy lewych punktów granicznych np.${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$2/3= 0,1222... ₃ = 0,1 2 ₃ = 0,2 0 ₃ i8/9= 0,21222... ₃ = 0,21 2 ₃ = 0,22 0 ₃ . Wszystkie te punkty końcowe są właściwymi ułamkami trójskładnikowymi (elementami ) postaci${\ Displaystyle \ mathbb {Z} \ cdot 3 ^ {- \ mathbb {N} _ {0}}}$P/Q, gdzie mianownik q jest potęgą 3, gdy ułamek ma postać nieredukowalną . Trójskładnikowa reprezentacja tych ułamków kończy się (tj. jest skończona) lub — przypomnijmy z góry, że każdy z właściwych ułamków trójskładnikowych ma 2 reprezentacje — jest nieskończona i „kończy się” albo nieskończenie wieloma powtarzającymi się zerami, albo nieskończenie wieloma powtarzającymi się dwójkami. Taki ułamek lewy punktu granicznego z jeśli jego trójskładnikowy reprezentacja nie zawiera 1 'a „kończy się” w nieskończenie wiele powtarzających 0s. Podobnie właściwy ułamek trójkowy jest właściwym punktem granicznym, jeśli ponownie jego rozwinięcie trójskładnikowe zawiera cyfry jedynek i „końcówki” w nieskończenie wielu powtarzających się dwójkach. ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Ten zestaw punktów końcowych jest gęsty w (ale nie gęsty w [0, 1]) i tworzy przeliczalnie nieskończony zestaw. Liczby, w których nie są punktami końcowymi, również mają tylko zera i 2 w swojej reprezentacji trójskładnikowej, ale nie mogą kończyć się nieskończonym powtórzeniem cyfry 0 ani cyfry 2, ponieważ wtedy byłby to punkt końcowy. ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Funkcja od do [0,1] jest zdefiniowana przez wzięcie liczb trójskładnikowych, które składają się wyłącznie z 0 i 2, zastąpienie wszystkich 2 przez 1 i interpretację sekwencji jako binarną reprezentację liczby rzeczywistej. W formule ${\displaystyle {\mathcal {C}}}$

${\ Displaystyle f {\ bigg (} \ suma _ {k \ w \ mathbb {N}} a_ {k} 3 ^ {-k} {\ bigg)} = \ suma _ {k \ w \ mathbb {N} }{\frac {a_{k}}{2}}2^{-k}}$   gdzie   ${\ Displaystyle \ forall k \ w \ mathbb {N}: a_ {k} \ w \ {0,2 \}}.$

Dla dowolnej liczby y w [0,1] jej binarną reprezentację można przetłumaczyć na trójskładnikową reprezentację liczby x in przez zastąpienie wszystkich 1s przez 2s. Z tym, f ( x ) = Y , tak że Y znajduje się w zakresie od f . Na przykład, jeśli y =${\displaystyle {\mathcal {C}}}$3/5= +0,100110011001 ... ₂ = 0. 1001 , piszemy x = 0. 2002 = 0.200220022002 ... ₃ =7/10. W konsekwencji f jest surjektywne. Jednak f nie jest iniektywna — wartości, dla których f ( x ) są zbieżne, to te znajdujące się na przeciwległych końcach jednej ze środkowych trzecich usuniętych. Na przykład weź

1/3= 0,0 2 ₃ (co oznacza prawy punkt graniczny i lewy punkt graniczny środkowej tercji [${\displaystyle {\mathcal {C}}}$1/3, 2/3]) oraz

2/3= 0,2 0 ₃ (czyli lewy punkt graniczny i prawy punkt graniczny środkowej tercji [${\displaystyle {\mathcal {C}}}$1/3, 2/3])

więc

${\ Displaystyle {\ zacząć {tablica} {lcl} f {\ bigl (}{} ^ {1} \! \! / \! _ {3} {\ duży )} = f (0,0 {\ nadkreślenie {2} }_{3})=0.0{\overline {1}}_{2}=\!\!&\!\!0.1_{2}\!\!&\!\!=0.1{\overline {0 }}_{2}=f(0.2{\overline {0}}_{3})=f{\bigl (}{}^{2}\!\!/\!_{3}{\bigr ) }.\\&\równolegle \\&{}^{1}\!\!/\!_{2}\end{array}}}$

Zatem w zbiorze Cantora jest tyle punktów, ile jest w przedziale [0, 1] (który ma niepoliczalną kardynalność ). Jednak zbiór punktów końcowych usuniętych przedziałów jest przeliczalny, więc w zbiorze Cantora musi być niepoliczalnie wiele liczb, które nie są punktami końcowymi przedziałów. Jak wspomniano powyżej, jednym z przykładów takiej liczby jest${\ Displaystyle {\ mathfrak {c}} = 2 ^ {\ aleph _ {0}}}$1/4, Który może być zapisany jako 0.020202 ... ₃ = 0. 02 w potrójnym notacji. W rzeczywistości, biorąc pod uwagę , istnieją takie, że . Po raz pierwszy zademonstrował to Steinhaus w 1917 roku, który udowodnił za pomocą argumentu geometrycznego równoważne twierdzenie, że dla każdego . Ponieważ ta konstrukcja zapewnia iniekcję od do , mamy bezpośredni wniosek. Zakładając, że dla każdego zbioru nieskończonego (oświadczenie okazały się równoznaczne z aksjomatu wyboru przez Tarskiego ), to zapewnia, że kolejną demonstrację . ${\displaystyle a\in [-1,1]}$${\displaystyle x,y\in {\mathcal {C}}}$${\displaystyle a=yx}$${\ Displaystyle \ {(x, y) \ w \ mathbb {R} ^ {2} \ mid y = x + a \} \; \ czapka \; ({\ mathcal {C}} \ razy {\ mathcal { C}})\neq \emptyset }$${\displaystyle a\in [-1,1]}$${\displaystyle [-1,1]}$${\ Displaystyle {\ mathcal {C}} \ razy {\ mathcal {C}}}$${\ Displaystyle | {\ mathcal {C}} \ razy {\ mathcal {C}} | \ geq | [-1, 1] | = {\ mathfrak {c}}}$${\displaystyle |A\razy A|=|A|}$${\ Displaystyle A}$${\ Displaystyle | {\ mathcal {C}} | = {\ mathfrak {c}}}$

Zbiór Cantora zawiera tyle punktów, ile wynosi przedział, z którego został wzięty, ale sam nie zawiera przedziału o niezerowej długości. Liczby niewymierne mają tę samą właściwość, ale zbiór Cantora ma dodatkową właściwość, że jest domknięty, więc nie jest nawet gęsty w żadnym przedziale, w przeciwieństwie do liczb niewymiernych, które są gęste w każdym przedziale.

Przypuszcza się, że wszystkie algebraiczne liczby niewymierne są normalne . Ponieważ elementy zbioru Cantora nie są normalne, oznaczałoby to, że wszystkie elementy zbioru Cantora są albo racjonalne, albo transcendentalne .

Samopodobieństwo

Zbiór Cantora jest prototypem fraktala . Jest samopodobny , ponieważ jest równy dwóm kopiom samego siebie, jeśli każda kopia jest zmniejszona o współczynnik 3 i przetłumaczona. Dokładniej, zbiór Cantora jest równy połączeniu dwóch funkcji, lewej i prawej transformacji samopodobieństwa samego siebie oraz , co pozostawia zbiór Cantora niezmiennikiem do homeomorfizmu :${\ Displaystyle T_ {L} (x) = x/3}$${\ Displaystyle T_ {R} (x) = (2 + x) / 3}$${\ Displaystyle T_ {L} ({\ mathcal {C}}) \ cong T_ {R} ({\ mathcal {C}}) \ cong {\ mathcal {C}} = T_ {L} ({\ mathcal { C}})\cup T_{R}({\mathcal {C}}).}$

Powtarzające iteracja od i mogą być wizualizowane jako nieskończonego drzewa binarnego . Oznacza to, że w każdym węźle drzewa można rozważyć poddrzewo po lewej lub po prawej stronie. Zestawienie wraz z kompozycją funkcji tworzy monoid , monoid diadyczny . ${\displaystyle T_{L}}$${\displaystyle T_{R}}$${\ Displaystyle \ {T_ {L}, T_ {R} \}}$

W automorfizmy drzewa binarnego hiperboliczne są jego obroty, a podane przez grupy modułowej . Zatem zbiór Cantora jest przestrzenią jednorodną w tym sensie, że dla dowolnych dwóch punktów iw zbiorze Cantora istnieje homeomorfizm z . Konstrukcję jawną można opisać łatwiej, jeśli zobaczymy zbiór Cantora jako przestrzeń iloczynu przeliczalnie wielu kopii przestrzeni dyskretnej . Wtedy mapa zdefiniowana przez jest homeomorfizmem inwolucyjnym zamieniającym się i . ${\displaystyle x}$${\displaystyle y}$${\displaystyle {\mathcal {C}}}$${\ Displaystyle h: {\ mathcal {C}} \ do {\ mathcal {C}}}$${\displaystyle h(x)=y}$${\ Displaystyle h}$${\ Displaystyle \ {0,1 \}}$${\ Displaystyle h: \ {0,1 \} ^ {\ mathbb {N}} \ do \ {0,1 \} ^ {\ mathbb {N}}}$${\ Displaystyle h_ {n} (u): = u_ {n} + x_ {n} + y_ {n} \ mod 2}$${\displaystyle x}$${\displaystyle y}$

Prawo konserwatorskie

Stwierdzono, że za skalowanie i samopodobieństwo zawsze odpowiada jakaś forma prawa zachowania. W przypadku zbioru Cantora widać, że moment (gdzie jest wymiarem fraktalnym) wszystkich zachowanych przedziałów na dowolnym etapie procesu konstrukcji jest równy stałej, która w przypadku zbioru Cantora jest równa jedności. Wiemy, że na etapie budowy systemu występują przedziały wielkości . Następnie, jeśli oznaczymy przedziały, które przeżyły, jako wtedy th moment jest od . ${\displaystyle d_{f}}$${\ Displaystyle d_ {f} = \ ln (2) / \ ln (3)}$${\ Displaystyle N = 2 ^ {n}}$${\ Displaystyle 1/3 ^ {n}}$${\ Displaystyle n}$${\ Displaystyle x_ {1}, x_ {2}, \ ldots, x_ {2 ^ {n}}}$${\displaystyle d_{f}}$${\ Displaystyle x_ {1} ^ {d_ {f}} + x_ {2} ^ {d_ {f}} + \ cdots + x_ {2 ^ {n}} ^ {d_ {f}} = 1}$${\ Displaystyle x_ {1} = x_ {2} = \ cdots = x_ {2 ^ {n}} = 1/3 ^ {n}}$

Wymiar Hausdorff zbioru Cantora wynosi ln (2) / ln (3) ≈ 0,631.

Właściwości topologiczne i analityczne

Chociaż „zbiór” Cantora zazwyczaj odnosi się do oryginalnego, środkowego Cantora opisanego powyżej, topologowie często mówią o zbiorze Cantora „zbiór”, który oznacza dowolną przestrzeń topologiczną, która jest z nim homeomorficzna (topologicznie równoważna).

Jak pokazuje powyższa argumentów podsumowanie, zbiór Cantora jest niezliczona ale ma miary Lebesgue'a 0. Ponieważ zbiór Cantora jest komplementarna do unii z zbiorów otwartych , to samo w sobie jest zamknięty podzbiór liczb rzeczywistych, a więc kompletna przestrzenią metryczną . Ponieważ jest ona również całkowicie ograniczona , twierdzenie Heinego-Borela mówi, że musi być zwarta .

Dla dowolnego punktu w zbiorze Cantora i dowolnego arbitralnie małego sąsiedztwa tego punktu istnieje jakaś inna liczba z liczebnikiem trójkowym składającym się tylko z zer i dwójek, jak również liczby, których liczebniki trójkowe zawierają jedynki. Stąd każdy punkt w zbiorze Cantora jest punktem skupienia (zwanym również punktem skupienia lub punktem granicznym) zbioru Cantora, ale żaden nie jest punktem wewnętrznym . Zbiór domknięty, w którym każdy punkt jest punktem skupienia, nazywany jest również zbiorem doskonałym w topologii , podczas gdy domknięty podzbiór przedziału bez punktów wewnętrznych nie jest nigdzie gęsty w przedziale.

Każdy punkt zbioru Cantora jest jednocześnie punktem skupienia dopełnienia zbioru Cantora.

Dla dowolnych dwóch punktów w zbiorze Cantora będzie jakaś cyfra trójczłonowa, w której się różnią — jeden będzie miał 0, a drugi 2. Dzieląc zbiór Cantora na „połówki” w zależności od wartości tej cyfry, otrzymujemy podział zbiór Cantora na dwa zamknięte zbiory, które oddzielają pierwotne dwa punkty. W topologii względnej zbioru Cantora punkty zostały oddzielone zbiorem clopen . W konsekwencji zestaw Cantora jest całkowicie odłączony . Jako kompaktowa, całkowicie odłączona przestrzeń Hausdorffa , zestaw Cantora jest przykładem przestrzeni Stone .

W przestrzeni topologicznej , zbiór Cantora jest naturalnie homeomorficzny do produktu z przeliczalnie wielu kopii przestrzeni , gdzie każda kopia niesie dyskretną topologię . To jest przestrzeń wszystkich ciągów w dwóch cyfrach ${\ Displaystyle \ {0,1 \}}$

${\ Displaystyle 2 ^ {\ mathbb {N}} = \ {(x_ {n}) \ mid x_ {n} \ w \ {0,1 \} {\ tekst {dla}} n \ w \ mathbb {N } \},}$

które można również utożsamiać ze zbiorem 2-adycznych liczb całkowitych . Podstawę dla otwartych zespołów topologii produktu są cylindryczne zestawy ; homeomorfizm odwzorowuje je na topologię podprzestrzenną, którą zbiór Cantora dziedziczy z naturalnej topologii na osi liczb rzeczywistych. Ta charakterystyka przestrzeni Cantora jako iloczynu przestrzeni zwartych daje drugi dowód, że przestrzeń Cantora jest zwarta, poprzez twierdzenie Tychonowa .

Z powyższej charakterystyki zbiór Cantora jest homeomorficzny z liczbami p-adycznymi , a po usunięciu jednego punktu z liczbami p-adycznymi .

Zbiór Cantora jest podzbiorem liczb rzeczywistych, które są przestrzenią metryczną w odniesieniu do zwykłej metryki odległości ; dlatego zbiór Cantora sam w sobie jest przestrzenią metryczną, używając tej samej metryki. Alternatywnie można użyć metryki p-adycznej na : przy danych dwóch sekwencjach odległość między nimi wynosi , gdzie jest najmniejszym indeksem takim, że ; jeśli nie ma takiego indeksu, to obie sekwencje są takie same, a jeden definiuje odległość jako zero. Te dwie metryki generują tę samą topologię w zbiorze Cantora. ${\ Displaystyle 2 ^ {\ mathbb {N} }}$${\ Displaystyle (x_ {n}), (y_ {n}) \ w 2 ^ {\ mathbb {N}}}$${\ Displaystyle d ((x_ {n}), (y_ {n})) = 2 ^ {-k}}$${\displaystyle k}$${\ Displaystyle x_ {k} \ neq y_ {k}}$

Widzieliśmy powyżej, że zestaw Cantora jest całkowicie odłączoną, idealną, kompaktową przestrzenią metryczną. Rzeczywiście, w pewnym sensie jest to jedyny: każda niepusta, całkowicie odłączona, idealna, zwarta przestrzeń metryczna jest homeomorficzna dla zbioru Cantora. Zobacz przestrzeń Cantora, aby dowiedzieć się więcej o przestrzeniach homeomorficznych dla zestawu Cantora.

Zbiór Cantora jest czasami postrzegane jako „uniwersalny” w kategorii od zwartych przestrzeni metrycznych , ponieważ każda przestrzeń metryczna zwarta jest obrazem ciągłym zbioru Cantora; jednak ta konstrukcja nie jest unikalna, a więc zbiór Cantora nie jest uniwersalny w ścisłym sensie kategorycznym. Własność „uniwersalna” ma ważne zastosowania w analizie funkcjonalnej , gdzie jest czasami znana jako twierdzenie o reprezentacji dla zwartych przestrzeni metrycznych .

Dla dowolnej liczby całkowitej q ≥ 2, topologia w grupie G= Z _q ^ω (przeliczalna suma bezpośrednia) jest dyskretna. Chociaż podwójna liczba Pontrjagin Γ jest również Z _q ^ω , topologia Γ jest zwarta. Widać, że Γ jest całkowicie oderwane i doskonałe - jest więc homeomorficzne w stosunku do zbioru Cantora. Najłatwiej wypisać homeomorfizm wprost w przypadku q =2. (Patrz Rudin 1962, s. 40.)

Średnia geometryczna zbioru Cantora wynosi około 0,274974.

Miara i prawdopodobieństwo

Zbiór Cantora może być postrzegany jako zwarta grupa ciągów binarnych i jako taki jest wyposażony w naturalną miarę Haara . Po znormalizowaniu tak, aby miara zbioru wynosiła 1, jest to model nieskończonej sekwencji rzutów monetą. Co więcej, można wykazać, że zwykła miara Lebesgue'a na interwale jest obrazem miary Haara na zbiorze Cantora, podczas gdy naturalne wstrzyknięcie do zbioru trójkowego jest kanonicznym przykładem miary osobliwej . Można również wykazać, że miara Haara jest obrazem dowolnego prawdopodobieństwa , co sprawia, że ​​Cantor wyznacza w pewien sposób uniwersalną przestrzeń prawdopodobieństwa.

W teorii miary Lebesgue'a zbiór Cantora jest przykładem zbioru niepoliczalnego i mającego miarę zerową.

Liczby kantora

Jeśli zdefiniujemy liczbę Cantora jako członka zbioru Cantora, to

1. Każda liczba rzeczywista w [0, 2] jest sumą dwóch liczb Cantora.
2. Pomiędzy dowolnymi dwoma liczbami Cantora znajduje się liczba, która nie jest liczbą Cantora.

Opisowa teoria mnogości

Zbiór Cantora jest zbiorem skromnym (lub zbiorem pierwszej kategorii) jako podzbiorem [0,1] (chociaż nie jako podzbiór samego siebie, ponieważ jest to przestrzeń Baire'a ). Zbiór Cantora pokazuje zatem, że pojęcia „wielkości” w kategoriach kardynalności, miary i kategorii (Baire) nie muszą się pokrywać. Podobnie jak zbiór , zbiór Cantora jest „mały” w tym sensie, że jest zbiorem zerowym (zbiór miary zero) i jest skromnym podzbiorem [0,1]. Jednak w przeciwieństwie do , które jest policzalne i ma „małą” kardynalność, , kardynalność jest taka sama jak [0,1], kontinuum i jest „duża” w sensie kardynalności. W rzeczywistości możliwe jest również skonstruowanie podzbioru [0,1], który jest skromny, ale o dodatniej mierze i podzbioru, który nie jest skromny, ale o zerowej mierze: Biorąc policzalną sumę „grubych” zbiorów miary Cantora (patrz zbiór Smith–Volterra–Cantor poniżej dla konstrukcji), otrzymujemy zbiór, który ma miarę dodatnią (równą 1), ale jest ubogi w [0,1], ponieważ żaden nie jest nigdzie gęsty. Następnie rozważ zestaw . Ponieważ , nie może być skromny, ale ponieważ , musi mieć miarę zero. ${\ Displaystyle \ mathbb {Q} \ czapka [0,1]}$${\displaystyle {\mathcal {C}}}$${\ Displaystyle \ mathbb {Q} \ czapka [0,1]}$${\displaystyle \aleph_{0}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathfrak {c}}}$${\ Displaystyle {\ mathcal {C}} ^ {(n)}}$${\ Displaystyle \ lambda = (n-1) / n}$${\textstyle {\mathcal {A}}:=\bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$${\ Displaystyle {\ mathcal {C}} ^ {(n)}}$${\textstyle {\mathcal {A}}^{\mathrm {c} }=[0,1]\setminus \bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n )}}$${\ Displaystyle {\ mathcal {A}} \ filiżanka {\ mathcal {A}} ^ {\ mathcal {c}} = [0,1]}$${\ Displaystyle {\ mathcal {A}} ^ {\ operatorname {c}}}$${\ Displaystyle \ mu ({\ mathcal {A}}) = 1}$${\ Displaystyle {\ mathcal {A}} ^ {\ operatorname {c}}}$

Warianty

Zestaw Smith–Volterra–Cantor

Zamiast wielokrotnie usuwać środkową trzecią część każdego elementu, jak w zestawie Cantora, moglibyśmy również usuwać dowolny inny stały procent (inny niż 0% i 100%) ze środka. W przypadku, gdy środek8/10przedziału zostanie usunięty, otrzymujemy niezwykle przystępny przypadek — zbiór składa się ze wszystkich liczb w [0,1], które można zapisać jako ułamek dziesiętny składający się wyłącznie z zer i dziewiątek. Jeśli na każdym etapie usuwany jest stały procent, to zbiór graniczny będzie miał miarę zero, ponieważ długość reszty jest taka sama jak dla dowolnego f takiego, że . ${\ Displaystyle (1-f) ^ {n} \ do 0}$${\displaystyle n\do \infty}$${\displaystyle 0<f\leq 1}$

Z drugiej strony, „grube zbiory Cantora” o dodatniej mierze mogą być generowane przez usuwanie mniejszych ułamków środka segmentu w każdej iteracji. W ten sposób można skonstruować zbiory homeomorficzne do zbioru Cantora, które mają dodatnią miarę Lebesgue'a, a jednocześnie nie są nigdzie gęste. Jeżeli odstęp od długości ( ) usuwa się ze środka każdego segmentu w n -tego iteracji, po czym całkowita długość jest usuwany , a zestaw ograniczające będą miały środki Lebesgue'a się . Zatem w pewnym sensie zbiór środkowych tercji Cantora jest przypadkiem granicznym z . Jeśli , to reszta będzie miała miarę dodatnią z . Przypadek jest znany jako zbiór Smith-Volterra-Cantor , który ma miarę Lebesgue'a . ${\ Displaystyle r ^ {n}}$${\displaystyle r\leq 1/3}$${\textstyle \sum _{n=1}^{\infty }2^{n-1}r^{n}=r/(1-2r)}$${\ Displaystyle \ lambda = (1-3r) / (1-2r)}$${\displaystyle r=1/3}$${\displaystyle 0<r<1/3}$${\displaystyle 0<\lambda <1}$${\ Displaystyle r=1/4}$${\ Displaystyle 1/2}$

Stochastyczny zestaw Cantora

Konstrukcję zbioru Cantora można modyfikować, dzieląc losowo zamiast po równo. Poza tym, aby uwzględnić czas, możemy podzielić tylko jeden z dostępnych interwałów na każdym kroku zamiast dzielić wszystkie dostępne interwały. W przypadku stochastycznego triadycznego zbioru Cantora wynikowy proces można opisać następującym równaniem szybkości

${\ Displaystyle {\ Frac {\ częściowy c (x, t)} {\ częściowy t}} = - {\ Frac {x ^ {2}} {2}} c (x, t) + 2 \ int _ { x}^{\infty }(yx)c(y,t)\,dy,}$

oraz dla stochastycznego dwuczłonowego zbioru Cantora

${\ Displaystyle {{\ częściowy c (x, t)} \ nad {\ częściowy t}} = -xc (x, t) + (1+ p) \ int _ {x} ^ {\ infty} c (y ,t)\,dy,}$

gdzie jest liczba przedziałów wielkości między a . W przypadku triadycznego zbioru Cantora wymiar fraktalny jest mniejszy niż jego deterministyczny odpowiednik . W przypadku stochastycznego dwuczłonowego zbioru Cantora wymiar fraktalny jest znowu mniejszy niż jego deterministycznego odpowiednika . W przypadku stochastycznego dwuadycznego zbioru Cantora rozwiązaniem dla eksponatów jest skalowanie dynamiczne, gdyż jego rozwiązaniem w limicie długoczasowym jest wymiar fraktalny stochastycznego dwuadycznego zbioru Cantora . W obu przypadkach, podobnie jak triadyczny zbiór Cantora, moment ( ) stochastycznego zbioru triadycznego i diadycznego zbioru Cantora również są wielkościami zachowanymi. ${\displaystyle c(x,t)dx}$${\displaystyle x}$${\displaystyle x+dx}$${\ Displaystyle 0.5616}$${\ Displaystyle 0,6309}$${\displaystyle p}$${\ Displaystyle \ ln (1 + p) / \ ln 2}$${\displaystyle c(x,t)}$${\ Displaystyle t ^ {-(1 + d_ {f})} e ^ {-xt}}$${\displaystyle d_{f}=p}$${\displaystyle d_{f}}$${\textstyle \int x^{d_{f}}c(x,t)\,dx={\text{stała}}}$

Pył Kantora

Cantor dust to wielowymiarowa wersja zestawu Cantor. Można go utworzyć, biorąc ze sobą skończony iloczyn kartezjański zbioru Cantora, czyniąc go przestrzenią Cantora . Podobnie jak zestaw Cantora, pył Cantora ma miarę zerową .

Progresja rekurencji kostek Cantora w kierunku pyłu Cantora

Pył Cantora (2D)

Pył Cantora (3D)

Innym dwuwymiarowym odpowiednikiem zestawu Cantora jest dywan Sierpińskiego , gdzie kwadrat jest podzielony na dziewięć mniejszych kwadratów, a środkowy usunięty. Pozostałe kwadraty są następnie dalej dzielone na dziewięć, a środek usuwany, i tak dalej w nieskończoność. Jednym z trójwymiarowych odpowiedników tego jest gąbka Mengera .

Uwagi historyczne

Kapitał kolumny ze wzorem przywodzącym na myśl zbiór Cantora, ale wyrażony raczej w postaci binarnej niż trójczłonowej. Grawerowanie Île de Philae z Description d'Égypte autorstwa Jean-Baptiste Prosper Jollois i Édouard Devilliers, Imprimerie Impériale, Paryż, 1809-1828

Sam Cantor zdefiniował zbiór w sposób ogólny, abstrakcyjny, a o konstrukcji trójskładnikowej wspomniał tylko mimochodem, jako przykład idei ogólniejszej, czyli zbioru doskonałego , nigdzie nie gęstego . W oryginalnym artykule przedstawiono kilka różnych konstrukcji koncepcji abstrakcyjnej.

Ten zestaw byłby uważany za abstrakcyjny w czasie, gdy tworzył go Cantor. Sam Cantor prowadził do tego praktyczne obawy dotyczące zbioru punktów, w których szereg trygonometryczny może nie być zbieżny. Odkrycie to w znacznym stopniu nastawiło go na drogę do opracowania abstrakcyjnej, ogólnej teorii zbiorów nieskończonych .

Zobacz też

• Funkcja wskaźnika zestawu Cantor
• Zestaw Smith–Volterra–Cantor
• Heksagramy (I Ching)
• Funkcja Kantora
• Kostka Kantora
• Naszyjnik Antoine
• Śnieżynka Koch
• Kibic Knaster–Kuratowski
• Lista fraktali według wymiaru Hausdorffa
• Sekwencja Moser-de Bruijna

Uwagi

Bibliografia

Zewnętrzne linki

• "Zestaw Cantora" , Encyklopedia Matematyki , EMS Press , 2001 [1994]
• Zestawy Cantora oraz Zestaw i funkcja Cantora przy przecięciu węzła
• Zestaw Kantora w Krainach Platońskich