Aksjomaty Tarskiego - Tarski's axioms

Aksjomaty Tarskiego , ze względu na Alfreda Tarskiego , są aksjomat zestaw do znacznego fragmentu geometrii euklidesowej , że jest formulable w logice pierwszego rzędu z tożsamości , i nie wymaga żadnej teorii mnogości ( Tarski 1959 ) (to znaczy, że część geometrii euklidesowej, że jest formulable jako elementarna teoria ). Inne nowoczesne axiomizations z geometrii euklidesowej są Aksjomatyka Hilberta i aksjomaty Birkhoffa .

Przegląd

Na początku swojej kariery Tarski uczył geometrii i badał teorię mnogości. Jego współpracownik Steven Givant (1999) wyjaśnił punkt startu Tarskiego:

Od Enriquesa Tarski dowiedział się o pracy Mario Pieri , włoskiego geometra, który był pod silnym wpływem Peano. Tarski wolał system Pieriego [jego pamiętnik Point and Sphere ], w którym struktura logiczna i złożoność aksjomatów były bardziej przejrzyste.

Givant mówi wtedy, że „z typową dokładnością” Tarski obmyślił swój system:

Co było innego w podejściu Tarskiego do geometrii? Po pierwsze, system aksjomatów był znacznie prostszy niż którykolwiek z dotychczasowych systemów aksjomatów. W rzeczywistości długość wszystkich aksjomatów Tarskiego razem jest niewiele więcej niż tylko jednym z 24 aksjomatów Pieriego. Był to pierwszy system geometrii euklidesowej na tyle prosty, że wszystkie aksjomaty dawały się wyrazić jedynie w terminach pojęć pierwotnych , bez pomocy pojęć zdefiniowanych. Co jeszcze ważniejsze, po raz pierwszy dokonano wyraźnego rozróżnienia między pełną geometrią a jej elementarną — to znaczy jej częścią pierwszego rzędu.

Podobnie jak inne nowoczesne aksjomatyzacje geometrii euklidesowej, Tarski posługuje się systemem formalnym składającym się z ciągów symboli, zwanych zdaniami , których konstrukcja respektuje formalne reguły syntaktyczne oraz reguły dowodu określające dozwolone manipulacje zdaniami. W przeciwieństwie do niektórych innych nowoczesnych aksjomatyzacji, takich jak Birkhoffa i Hilberta , aksjomatyzacja Tarskiego nie ma żadnych obiektów pierwotnych innych niż punkty , więc zmienna lub stała nie może odnosić się do prostej lub kąta. Ponieważ punkty są jedynymi obiektami pierwotnymi, a system Tarskiego jest teorią pierwszego rzędu , nie jest nawet możliwe zdefiniowanie prostych jako zbiorów punktów. Jedyne pierwotne relacje ( predykaty ) to „pomiędzy” i „kongruencja” między punktami.

Aksjomatyzacja Tarskiego jest krótsza niż jej rywale, co w pewnym sensie podkreślają Tarski i Givant (1999). Jest bardziej zwięzły niż Pieri, ponieważ Pieri miał tylko dwa prymitywne pojęcia, podczas gdy Tarski wprowadził trzy: punkt, pomiędzy i zgodność. Taka ekonomia pojęć pierwotnych i zdefiniowanych oznacza, że ​​system Tarskiego nie jest zbyt wygodny do robienia geometrii euklidesowej. Tarski zaprojektował swój system raczej, aby ułatwić jego analizę za pomocą narzędzi logiki matematycznej , tj. aby ułatwić wyprowadzenie jego właściwości metamatematycznych. System Tarskiego ma niezwykłą właściwość polegającą na tym, że wszystkie zdania mogą być pisane w formie uniwersalno-egzystencjalnej, w szczególnym przypadku prenex normalnej formy . Ta forma ma wszystkie uniwersalne kwantyfikatory poprzedzające wszelkie kwantyfikatory egzystencjalne , tak że wszystkie zdania mogą być przetworzone w postaci. Fakt ten pozwolił Tarskiemu udowodnić, że geometria euklidesowa jest rozstrzygalna : istnieje algorytm, który może określić prawdziwość lub fałszywość dowolnego zdania. Aksjomatyzacja Tarskiego również jest kompletna . Nie stoi to w sprzeczności z pierwszym twierdzeniem Gödla o niezupełności , ponieważ teorii Tarskiego brakuje mocy ekspresyjnej potrzebnej do interpretacji arytmetyki Robinsona ( Franzén 2005 , s. 25–26). ${\ Displaystyle \ forall u \ forall v \ ldots \ istnieje a \ istnieje b \ kropki.}$

Aksjomaty

Alfred Tarski pracował nad aksjomatyzacją i metamatematyką geometrii euklidesowej z przerwami od 1926 do śmierci w 1983 roku, przy czym Tarski (1959) zapowiadał jego dojrzałe zainteresowanie tym tematem. Kulminacją prac Tarskiego i jego uczniów nad geometrią euklidesową była monografia Schwabhäuser, Szmielew i Tarski (1983), w której przedstawiono 10 aksjomatów i jeden schemat aksjomatów pokazanych poniżej, związaną z nimi metamatematykę i sporo tematu. Gupta (1965) wniósł istotny wkład, a Tarski i Givant (1999) omawiają historię.

Podstawowe relacje

Te aksjomaty są bardziej elegancką wersją zbioru opracowanego przez Tarskiego w latach dwudziestych XX wieku jako część jego badań metamatematycznych właściwości geometrii płaszczyzny euklidesowej . Cel ten wymagał przeformułowania tej geometrii jako teorii pierwszego rzędu . Tarski tak więc przez positing się wszechświat z punktów , z małych liter oznaczających zmiennych występujących na tym wszechświecie. Równość jest zapewniana przez podstawową logikę (zobacz Logika pierwszego rzędu#Równość i jej aksjomaty ). Tarski następnie zaproponował dwie pierwotne relacje:

• Pomiędzy , relacja triadyczna . Zdanie atomowy Bxyz oznacza, że Y jest „pomiędzy”, X i Z , innymi słowy, że Y jest punktem na odcinku liniowym XZ . (Ta relacja jest interpretowana włącznie, tak że Bxyz jest trywialnie prawdziwe, gdy x=y lub y=z ).
• Congruence (lub „równej odległości”), relacja tetradyczna . Zdanie atomowy wx ≡ YZ może być interpretowane jako wx znaczy przystające do YZ , innymi słowy, że długość odcinka linii WX jest równa długości odcinka linii YZ .

Pomiędzy ujmuje afiniczny aspekt geometrii euklidesowej; kongruencja, jej aspekt metryczny . Logika tła zawiera tożsamość , relację binarną . Aksjomaty przywołują tożsamość (lub jej negację) w pięciu przypadkach.

Poniższe aksjomaty są pogrupowane według typów relacji, które wywołują, a następnie posortowane, najpierw według liczby kwantyfikatorów egzystencjalnych, a następnie według liczby zdań atomowych. Aksjomaty należy odczytywać jako uniwersalne domknięcia ; stąd wszelkie wolne zmienne powinny być traktowane jako milcząco uniwersalnie kwantyfikowane .

Aksjomaty kongruencji

Refleksywność kongruencji

${\displaystyle xy\equivyx\,.}$

Tożsamość kongruencji

${\displaystyle xy\equivzz\rightarrow x=y.}$

Przechodniość kongruencji

${\displaystyle (xy\equiv zu\land xy\equivvw)\rightarrow zu\equivvw.}$

Komentarz

Podczas gdy relacja kongruencji jest formalnie czterostronną relacją między punktami, nieformalnie można ją również traktować jako binarną relację między dwoma odcinkami linii i . Powyższe aksjomaty „zwrotności” i „przechodniości” dowodzą obu: ${\displaystyle xy\equiv zw}$${\displaystyle xy}$${\displaystyle zw}$

• że ta relacja binarna jest w rzeczywistości relacją równoważności
  • jest refleksyjny: .${\displaystyle xy\ekwiwalent xy}$
  • jest symetryczny .${\displaystyle xy\equiv zw\rightarrow zw\equivxy}$
  • jest przechodnia .${\displaystyle (xy\equiv zu\land zu\equivvw)\rightarrow xy\equivvw}$
• a kolejność, w jakiej są określane punkty odcinka linii, jest nieistotna.
  • ${\displaystyle xy\equiv zw\rightarrow xy\equivwz}$.
  • ${\displaystyle xy\equiv zw\rightarrow yx\equiv zw}$.
  • ${\displaystyle xy\equiv zw\rightarrow yx\equivwz}$.

Aksjomat „przechodniości” zakłada , że kongruencja jest euklidesowa , ponieważ respektuje pierwsze z „ wspólnych pojęć ” Euklidesa .

Aksjomat „tożsamości zgodności” intuicyjnie stwierdza, że ​​jeśli xy jest przystające z segmentem, który zaczyna się i kończy w tym samym punkcie, to x i y są tym samym punktem. Jest to ściśle związane z pojęciem zwrotności dla relacji binarnych .

Aksjomaty pomiędzy

Aksjomat Pascha

Tożsamość Pomiędzy

${\displaystyle Bxyx\rightarrow x=y.}$

Jedynym punktem na tym odcinku jest sam. ${\ Displaystyle xx}$${\displaystyle x}$

Aksjomat Paschy

${\ Displaystyle (Bxuz \ land Byvz) \ rightarrow \ istnieje \ (Buay \ land Bvax).}$

Ciągłość: φ i ψ dzielą promień na dwie połowy, a aksjomat potwierdza istnienie punktu b dzielącego te dwie połowy

Schemat aksjomat ciągłości

Niech φ( x ) i ψ( y ) będą formułami pierwszego rzędu nie zawierającymi wolnych wystąpień ani a ani b . Niech nie będzie też wolnych wystąpień x w ( y ) lub y w φ( x ). Wtedy wszystkie instancje poniższego schematu są aksjomatami:

${\displaystyle \istnieje a\,\forall x\,\forall y\,[(\phi (x)\land \psi (y))\rightarrow Baxy]\rightarrow \istnieje b\,\forall x\,\ forall y\,[(\phi (x)\land \psi (y))\rightarrow Bxby].}$

Niech r będzie promieniem z punktem końcowym a . Niech wzory pierwszego rzędu φ i ψ definiują podzbiory X i Y z r , takie, że każdy punkt w Y znajduje się na prawo od każdego punktu X (w odniesieniu do a ). Wtedy istnieje punkt b w r leżący pomiędzy X i Y . Jest to zasadniczo konstrukcja cięcia Dedekinda , przeprowadzona w sposób, który pozwala uniknąć kwantyfikacji w zestawach.

Dolny wymiar

${\ Displaystyle \ istnieje a \ \ istnieje b \ \ istnieje c \, [\ neg Babc \ ziemia \ neg Bbca \ ziemia \ neg Bcab].}$

Istnieją trzy punkty niewspółliniowe. Bez tego aksjomatu teoria mogłaby być modelowana za pomocą jednowymiarowej prostej rzeczywistej , pojedynczego punktu, a nawet zbioru pustego.

Kongruencja i wzajemność

Wymiar górny

Wymiar górny

${\displaystyle (xu\equiv xv\land yu\equiv yv\land zu\equivzv\landu\neq v)\rightarrow (bxyz\lor byzx\lor bzxy).}$

Trzy punkty równoodległe od dwóch różnych punktów tworzą linię. Bez tego aksjomatu teoria mogłaby być modelowana przez przestrzeń trójwymiarową lub wyżej wymiarową.

Aksjomat Euklidesa

Każdy z trzech wariantów tego aksjomatu, wszystkie równoważne w stosunku do pozostałych aksjomatów Tarskiego z równoległym postulatem Euklidesa , ma przewagę nad innymi:

• A rezygnuje z egzystencjalnych kwantyfikatorów ;
• B ma najmniej zmiennych i zdań niepodzielnych ;
• C wymaga tylko jednego prymitywnego pojęcia, pomiędzy. Ten wariant jest zwykle podawany w literaturze.

O :${\ Displaystyle ((Bxyw\land xy\equiv yw) \land (Bxuv\land xu\equiv uv)\land (Byuz\land yu\equiv zu))\rightarrow yz\equiv vw.}$

Niech odcinek linii łączy punkt środkowy dwóch boków danego trójkąta . Ten odcinek linii będzie o połowę krótszy niż trzeci bok. Odpowiada to wewnętrznym kątom dowolnego trójkąta sumującym się do dwóch kątów prostych .

B :${\ Displaystyle Bxyz \ lor Byzx \ lor Bzxy \ lor \ istnieje a \ (xa \ equiv ya \ land xa \ equiv za).}$

Mając dowolny trójkąt , istnieje okrąg, który zawiera wszystkie jego wierzchołki.

Aksjomat Euklidesa: C

C :${\ Displaystyle (Bxuv \ ziemia Byuz \ ziemia x \ neq u) \ rightarrow \ istnieje a \ \ istnieje b \ (Bxya \ ziemia Bxzb \ ziemia Bavb).}$

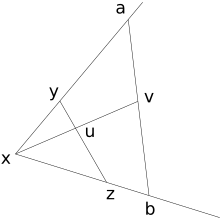
Mając dowolny kąt i dowolny punkt v w jego wnętrzu, istnieje odcinek zawierający v , z punktem końcowym po każdej stronie kąta.

Pięć segmentów

Pięć segmentów

${\displaystyle {(x\neq y\land Bxyz\land Bx'y'z'\land xy\equiv x'y'\land yz\equiv y'z\land xu\equiv x'u'\land yu \equiv y'u')}\rightarrow zu\equiv z'u'.}$

Zacznij od dwóch trójkątów , xuz i x'u'z'. Narysuj odcinki linii yu i y'u', łącząc wierzchołek każdego trójkąta z punktem po przeciwnej stronie wierzchołka. Rezultatem są dwa podzielone trójkąty, z których każdy składa się z pięciu segmentów. Jeśli cztery segmenty jednego trójkąta są przystające do segmentu w drugim trójkącie, to piąty segment w obu trójkątach musi być przystający.

Jest to równoważne regule kąt boczny-bok określający, że dwa trójkąty są przystające; jeśli kąty uxz i u'x'z' są przystające (istnieją przystające trójkąty xuz i x'u'z' ), a dwie pary boków wypadających są przystające ( xu ≡ x'u' i xz ≡ x'z ' ), to pozostała para boków również jest przystająca ( uz ≡ u'z ).

Budowa segmentu

${\ Displaystyle \ istnieje z \, [Bxyz \ ziemia yz \ równoważnik ab].}$

Dla dowolnego punktu y można narysować w dowolnym kierunku (określonym przez x ) prostą przystającą do dowolnego odcinka ab .

Dyskusja

Zaczynając od dwóch pierwotnych stosunków , których pola są gęste wszechświat z punktów , Tarski zbudował geometrię odcinków . Według Tarskiego i Givanta (1999: 192-93) żaden z powyższych aksjomatów nie jest zasadniczo nowy. Pierwsze cztery aksjomaty ustalają pewne elementarne własności dwóch relacji pierwotnych. Na przykład, Reflexivity i Transitivity of Congruence ustalają, że zgodność jest relacją równoważności na odcinkach linii. Tożsamość kongruencji i wzajemności rządzi trywialnym przypadkiem, gdy te relacje stosuje się do nierozróżnialnych punktów. Twierdzenie xy ≡ zz ↔ x = y ↔ Bxyx rozszerza te aksjomaty tożsamości.

Szereg innych właściwości Pomiędzy można wyprowadzić jako twierdzenia, w tym:

• Refleksyjność : Bxxy  ;
• Symetria : Bxyz → Bzyx  ;
• Przechodniość : ( Bxyw ∧ Byzw ) → Bxyz  ;
• Łączność : ( Bxyw ∧ Bxzw ) → ( Bxyz ∨ Bxzy ).

Dwie ostatnie właściwości całkowicie porządkują punkty tworzące odcinek linii.

Wymiar górny i dolny razem wymagają, aby każdy model tych aksjomatów miał określoną, skończoną wymiarowość . Odpowiednie zmiany w tych aksjomatach dają zbiory aksjomatów dla geometrii euklidesowej dla wymiarów 0, 1 i większych niż 2 (Tarski i Givant 1999: Aksjomaty 8 ⁽¹⁾ , 8 ⁽ⁿ⁾ , 9 ⁽⁰⁾ , 9 ⁽¹⁾ , 9 ^{( n)} ). Zauważ, że geometria bryłowa nie wymaga nowych aksjomatów, w przeciwieństwie do aksjomatów Hilberta . Co więcej, Dolny Wymiar dla n wymiarów jest po prostu negacją Górnego Wymiaru dla n -1 wymiarów.

Gdy liczba wymiarów jest większa niż 1, Pomiędzy można zdefiniować w kategoriach zgodności (Tarski i Givant, 1999). Najpierw zdefiniuj relację „≤” (gdzie jest interpretowane „długość odcinka linii jest mniejsza lub równa długości odcinka ”): ${\displaystyle ab\leq cd}$${\displaystyle ab}$${\displaystyle cd}$

${\displaystyle xy\leq zu\leftrightarrow \forall v(zv\equiv uv\rightarrow \istnieje w(xw\equivyw\land yw\equiv uv)).}$

W przypadku dwóch wymiarów intuicja jest następująca: Dla dowolnego odcinka linii xy , rozważ możliwy zakres długości xv , gdzie v jest dowolnym punktem na dwusiecznej prostopadłej do xy . Oczywiste jest, że chociaż nie ma górnego ograniczenia długości xv , istnieje dolne ograniczenie, które występuje, gdy v jest środkiem xy . Więc jeśli xy jest krótsze lub równe zu , wtedy zakres możliwych długości xv będzie nadzbiorem zakresu możliwych długości zw , gdzie w jest dowolnym punktem na dwusiecznej prostopadłej zu .

Pomiędzy dwoma punktami można następnie określić, korzystając z intuicji, że najkrótszą odległością między dowolnymi dwoma punktami jest linia prosta:

${\ Displaystyle Bxyz \ leftrightarrow \ forall u ((ux \ leq xy \ land uz \ leq zy) \ rightarrow u = y).}$

Aksjomat schematu ciągłości zapewnia, że ​​uporządkowanie punktów na prostej jest kompletne (w odniesieniu do definiowalnych własności pierwszego rzędu). Aksjomaty Pascha i Euklidesa są dobrze znane. Co ciekawe, geometria euklidesowa wymaga tylko następujących dalszych aksjomatów:

• Budowa segmentu . Aksjomat ten umożliwia pomiar i kartezjański układ współrzędnych — po prostu przypisz wartość 1 do dowolnego, niepustego odcinka;

Niech wff oznacza dobrze sformułowaną formułę (lub formułę poprawną składniowo) geometrii elementarnej. Tarski i Givant (1999: 175) udowodnili, że elementarna geometria to:

• Konsekwentny : Nie ma takiego wff, aby zarówno on, jak i jego negacja były twierdzeniami;
• Complete : Każde zdanie lub jego negacja jest twierdzeniem dowodzącym z aksjomatów;
• Decydowalny : istnieje algorytm, który przypisuje każdemu zdaniu wartość prawdy . Wynika to z Tarskiego:
  • Procedura decyzyjna dla rzeczywistego ciała domkniętego , które znalazł przez eliminację kwantyfikatorową ( twierdzenie Tarskiego-Seidenberga );
  • Aksjomaty dopuszczające (wielowymiarowo) wierną interpretację jako rzeczywiste pole zamknięte .

Gupta (1965) udowodnił, że powyższe aksjomaty są niezależne, z wyjątkiem Pascha i refleksyjności zgodności .

Zanegowanie aksjomatu Euklidesa daje geometrię hiperboliczną , podczas gdy jego całkowite wyeliminowanie daje geometrię absolutną . Pełna (w przeciwieństwie do elementarnej) geometria euklidesowa wymaga rezygnacji z aksjomatyzacji pierwszego rzędu: zamień φ( x ) i ψ( y ) w schemacie aksjomatycznym Ciągłości na x ∈ A i y ∈ B , gdzie A i B są zmiennymi uniwersalnie kwantyfikowanymi przekraczający zestawy punktów.

Porównanie z Hilbertem

Aksjomaty Hilberta dla geometrii płaszczyzny numer 16 i obejmują przechodniość kongruencji i wariant aksjomatu Pascha. Jedynym pojęciem z geometrii intuicyjnej przywoływanym w uwagach do aksjomatów Tarskiego jest trójkąt . (Wersje B i C aksjomatu Euklidesa odnoszą się odpowiednio do „okręgu” i „kąta”). Aksjomaty Hilberta wymagają również „promienia”, „kąta” i pojęcia trójkąta „zawierającego” kąt. Oprócz pomiędzy i zgodności, aksjomaty Hilberta wymagają pierwotnej binarnej relacji „on”, łączącej punkt i linię. Axiom schematu Ciągłość odgrywa rolę podobną do dwóch Aksjomatyka Hilberta ciągłości. Ten schemat jest niezbędny; Geometria euklidesowa w języku Tarskiego (lub jego odpowiedniku) nie może być skończona aksjomatyzowana jako teoria pierwszego rzędu . Aksjomaty Hilberta nie stanowią teorii pierwszego rzędu, ponieważ jego aksjomaty ciągłości wymagają logiki drugiego rzędu .

Pierwsze cztery grupy aksjomatów aksjomatów Hilberta dla geometrii płaskiej są biinterpretowalne z aksjomatami Tarskiego minus ciągłość.

Zobacz też

• Geometria euklidesowa
• Przestrzeń euklidesowa

Uwagi

Bibliografia

• Franzén, Torkel (2005), Twierdzenie Gödla: niekompletny przewodnik po jego użyciu i nadużyciach , AK Peters, ISBN 1-56881-238-8
• Givant, Steven (1999) „Ujednolicenie wątków w pracy Alfreda Tarskiego”, Mathematical Intelligencer 21:47-58.
• Gupta, HN (1965) Wkład w Aksjomatyczne Podstawy Geometrii . doktorat praca dyplomowa na Uniwersytecie Kalifornijskim w Berkeley.
• Tarski, Alfred (1959), „Co to jest geometria elementarna?”, w Leon Henkin, Patrick Suppes i Alfred Tarski (red.), Metoda aksjomatyczna. Ze szczególnym uwzględnieniem geometrii i fizyki. Materiały z Międzynarodowego Sympozjum na Uniwersytecie im. z Kalifornii, Berkeley, 26 grudnia 1957-styczeń. 4, 1958 , Studies in Logic and the Foundations of Mathematics , Amsterdam: North-Holland, s. 16-29, MR  0106185. Dostępny jako przedruk 2007 , Brouwer Press, ISBN  1-4437-2812-8
• Alfred Tarski ; Givant, Steven (1999), "System geometrii Tarskiego", Biuletyn Logiki Symbolicznej , 5 (2): 175-214, CiteSeerX  10.1.1.27.9012 , doi : 10.2307/421089 , ISSN  1079-8986 , JSTOR  421089 , MR  1791303
• Schwabhäuser W., Szmielew W. i Alfred Tarski , 1983. Metamathematische Methoden in der Geometrie . Springer-Verlag.
• Szczerba, LW (1986). „Tarski i geometria”. Dziennik Logiki Symbolicznej . 51 (4): 907–12. doi : 10.2307/2273904 . JSTOR  2273904 .