Czworokąt styczny — Tangential quadrilateral

W geometrii euklidesowej , A stycznej czworoboku (czasami tylko styczny czworoboczny ) lub dobrze określone czworoboku jest A wypukła w kształcie czworoboku , którego boki wszystkie mogą być styczne do jednego koła w czworokącie. Ten krąg jest nazywany incircle w kształcie czworoboku lub jego wpisanego koła, jego centrum jest incenter a jej promień jest nazywany inradius . Ponieważ te czworoboki można wyciągnąć otaczający lub otaczające ich incircles, mają również nazywany circumscribable czworoboki , opisującego czworoboki i circumscriptible czworoboki . Czworokąty styczne są szczególnym przypadkiem wielokątów stycznych .

Inne rzadziej stosowane nazwy dla tej klasy czworoboków są inscriptable czworoboku , inscriptible czworoboku , Inskrybowany czworoboku , circumcyclic czworoboku i współ-cykliczny czworoboku . Ze względu na ryzyko pomylenia z czworokątem z okręgiem opisanym w okręgu, zwanym czworokątem cyklicznym lub czworobokiem wpisanym, lepiej nie używać żadnego z pięciu ostatnich nazw.

Wszystkie trójkąty mogą mieć okrąg, ale nie wszystkie czworoboki mają. Przykładem czworoboku, który nie może być styczny, jest prostokąt niekwadratowy . Poniższa charakterystyka przekroju określa, jakie konieczne i wystarczające warunki musi spełniać czworobok, aby mógł mieć okrąg.

Przypadki specjalne

Przykładami czworokątów stycznych są latawce , do których należą romb , który z kolei zawiera kwadraty . Latawce są dokładnie czworokątami stycznymi, które są również ortoprzekątne . Prawo latawiec to latawiec z circumcircle . Jeśli czworokąt jest zarówno styczny, jak i cykliczny , nazywany jest czworokątem dwucentrycznym , a jeśli jest zarówno styczny, jak i trapezowy , nazywany jest trapezem stycznym .

Charakterystyki

W stycznym czworoboku cztery dwusieczne kąta spotykają się w środku okręgu. Odwrotnie, wypukły czworobok, w którym cztery dwusieczne kąta spotykają się w punkcie, musi być styczny, a punktem wspólnym jest środek.

Zgodnie z twierdzeniem Pitota , dwie pary przeciwległych stronach stycznym czworoboku sumują się do tej samej długości całkowitej, co odpowiada semiperimeter s czworokąta:

${\ Displaystyle a + c = b + d = {\ Frac {a + b + c + d} {2}} = s.}$

Odwrotnie wypukły czworokąt, w którym a + c = b + d musi być styczne.

Jeżeli przeciwległe boki czworokąta wypukłego ABCD (czyli nie trapezu ) przecinają się w punktach E i F , to jest on styczny wtedy i tylko wtedy, gdy którykolwiek z

${\displaystyle \displaystyle BE+BF=DE+DF}$

lub

${\ Displaystyle \ Displaystyle AE-EC = AF-FC.}$

Drugi z nich jest prawie taki sam jak jedno z równości w twierdzeniu Urquharta . Jedyne różnice to znaki po obu stronach; w twierdzeniu Urquharta są sumy zamiast różnic.

Innym koniecznym i wystarczającym warunkiem jest to, że wypukły czworokąt ABCD jest styczny wtedy i tylko wtedy, gdy okręgi w dwóch trójkątach ABC i ADC są do siebie styczne .

Charakterystyka kątów tworzonych przez przekątną BD i cztery boki czworoboku ABCD wynika z Iosifescu. Udowodnił w 1954, że wypukły czworobok ma okrąg wtedy i tylko wtedy, gdy

${\ Displaystyle \ tan {\ Frac {\ kąt ABD} {2}} \ cdot \ tan {\ Frac {\ kąt BDC} {2}} = \ tan {\ Frac {\ kąt ADB} {2}} \ cdot \tan {\frac {\angle DBC}{2}}.}$

Ponadto czworokąt wypukły z kolejnymi bokami a , b , c , d jest styczny wtedy i tylko wtedy, gdy

${\ Displaystyle R_ {a} R_ {c} = R_ {b} R_ {d}}$

gdzie R _a , R _b , R _c , R _d są promienie zewnętrzne w kręgach styczna do boków , b , c , d , odpowiednio, a przedłużenie przyległych dwóch stron na każdym boku.

Kilka innych charakteryzacji jest znanych w czterech podtrójkątach utworzonych przez przekątne.

Specjalne segmenty linii

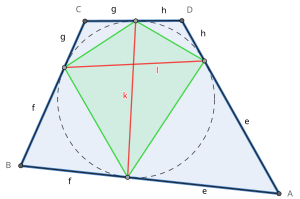
Osiem długości stycznych ( e , f , g , h na rysunku po prawej) czworokąta stycznego to odcinki linii od wierzchołka do punktów, w których okręg jest styczny do boków. Z każdego wierzchołka są dwie przystające długości styczne.

Dwa styczne cięciwy ( k i l na rysunku) stycznego czworoboku to odcinki linii, które łączą punkty po przeciwnych stronach, gdzie okrąg jest styczny do tych boków. Są to również przekątne tego czworokąta kontaktowego .

Obszar

Wzory nietrygonometryczne

Obszar K stycznej czworoboku jest przez

${\displaystyle \displaystyle K=r\cdot s}$

gdzie s to półobwód, a r to promień . Inna formuła to

${\ Displaystyle \ Displaystyle K = {\ tfrac {1} {2}} {\ sqrt {p ^ {2} q ^ {2} - (ac-BD) ^ {2}}}}$

co daje pole w postaci przekątnych p , q i boków a , b , c , d czworoboku stycznego.

Obszar można również wyrazić za pomocą tylko czterech długości stycznych . Jeżeli są to e , f , g , h , to czworokąt styczny ma pole

${\ Displaystyle \ Displaystyle K = {\ sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.}$

Ponadto powierzchnię czworoboku stycznego można wyrazić za pomocą boków a, b, c, d oraz kolejnych długości stycznych e, f, g, h jako

${\ Displaystyle K = {\ sqrt {abcd-(np.-fh) ^ {2}}}.}$

Ponieważ np = fh wtedy i tylko wtedy, gdy czworokąt styczny jest również cykliczny, a zatem dwucentryczny, pokazuje to, że maksymalna powierzchnia występuje wtedy i tylko wtedy, gdy czworokąt styczny jest dwucentryczny. ${\displaystyle {\sqrt {abcd}}}$

Wzory trygonometryczne

Wzór trygonometryczny na pole w odniesieniu do boków a , b , c , d i dwóch przeciwnych kątów to

${\displaystyle \displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}} .}$

Dla danych długości boków obszar jest maksymalny, gdy czworokąt jest również cykliczny, a zatem jest czworobokiem dwucentrycznym . Wtedy przeciwne kąty są kątami uzupełniającymi . Można to udowodnić w inny sposób używając rachunku różniczkowego . ${\ Displaystyle K = {\ sqrt {abcd}}}$

Innym wzorem na pole stycznego czworokąta ABCD, w którym występują dwa przeciwne kąty, jest

${\ Displaystyle K = \ po lewej (IA \ cdot IC + IB \ cdot ID \ po prawej) \ grzech {\ Frac {A + C} {2}}}$

gdzie ja jestem centrum.

W rzeczywistości obszar można wyrazić za pomocą tylko dwóch sąsiednich boków i dwóch przeciwnych kątów, jako

${\ Displaystyle K = ab \ sin {\ Frac {B} {2}} \ csc {\ Frac {D} {2}} \ grzech {\ Frac {B + D} {2}}.}$

Jeszcze inna formuła obszaru to

${\ Displaystyle K = {\ tfrac {1} {2}} | (ac-bd) \ tan {\ theta} |,}$

gdzie θ jest jednym z kątów między przekątnymi. Ten wzór nie może być użyty, gdy czworokąt styczny jest latawcem, ponieważ wtedy θ wynosi 90°, a funkcja styczna nie jest zdefiniowana.

Nierówności

Jak pośrednio zaznaczono powyżej, pole czworoboku stycznego o bokach a , b , c , d spełnia

${\displaystyle K\leq {\sqrt {abcd}}}$

z równością wtedy i tylko wtedy, gdy jest to dwucentryczny czworobok .

Według TA Ivanova 1976 (w), to semiperimeter s stycznej czworoboku spełnia

${\displaystyle s\geq 4r}$

gdzie r jest promieniem. Istnieje równość wtedy i tylko wtedy, gdy czworokąt jest kwadratem . Oznacza to, że dla obszaru K = rs istnieje nierówność

${\ Displaystyle K \ geq 4r ^ {2}}$

z równością wtedy i tylko wtedy, gdy czworokąt styczny jest kwadratem.

Właściwości partycji

Cztery odcinki linii pomiędzy środkiem incircle a punktami stycznymi do czworokąta dzielą czworokąt na cztery prawe latawce .

Jeżeli A nacięcia linia styczna czworoboczne na dwie wielokąta z równymi obszarach i jednakowych obwodów , to przewód przechodzi przez incenter .

Promień

Promień w czworoboku stycznym z kolejnymi bokami a , b , c , d jest określony wzorem

${\ Displaystyle r = {\ Frac {K} {s}} = {\ Frac {K} {a + c}} = {\ Frac {K} {b + d}}}$

gdzie K to pole czworoboku, a s to jego półobwód. W przypadku czworokąta stycznego z określonymi bokami promień wewnętrzny jest maksymalny, gdy czworokąt jest również cykliczny (a zatem jest czworokątem dwucentrycznym ).

Pod względem długości stycznej okrąg ma promień

${\displaystyle \displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}}.}$

Promień można również wyrazić w postaci odległości od środka I do wierzchołków czworoboku stycznego ABCD . Jeśli u = AI , v = BI , x = CI i y = DI , to

${\ Displaystyle r = 2 {\ sqrt {\ Frac {(\ sigma -uvx) (\ sigma -vxy) (\ sigma -xyu) (\ sigma -yuv)}{uvxy (uv + xy) (ux + vy) (uy+vx)}}}}$

gdzie . ${\ Displaystyle \ sigma = {\ tfrac {1} {2}} (uvx + vxy + xyu + yuv)}$

Jeżeli okręgi w trójkątach ABC , BCD , CDA , DAB mają odpowiednio promienie , to promień czworokąta stycznego ABCD jest określony wzorem${\displaystyle r_{1},r_{2},r_{3},r_{4}}$

${\ Displaystyle r = {\ Frac {G + {\ sqrt {G ^ {2}-4r_ {1} r_ {2} r_ {3} r_ {4} (r_ {1} r_ {3} + r_ {2} r_{4})}}}{2(r_{1}r_{3}+r_{2}r_{4})}}}$

gdzie . ${\displaystyle G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{ 1}r_{2}}$

Wzory kątów

Jeżeli e , f , g i h są długościami stycznymi od wierzchołków A , B , C i D odpowiednio do punktów , w których okrąg jest styczny do boków czworokąta stycznego ABCD , to kąty czworokąta można obliczyć z

${\ Displaystyle \ sin {\ Frac {A} {2}} = {\ sqrt {\ Frac {efg + fgh + ghe + hef} {(e + f) (e + g) (e + h)}}} ,}$

${\ Displaystyle \ sin {\ Frac {B} {2}} = {\ sqrt {\ Frac {efg + fgh + ghe + hef} {(f + e) ​​(f + g) (f + h)}}} ,}$

${\ Displaystyle \ sin {\ Frac {C} {2}} = {\ sqrt {\ Frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}} ,}$

${\ Displaystyle \ sin {\ Frac {D} {2}} = {\ sqrt {\ Frac {efg + fgh + ghe + hef} {(h + e) ​​(h + f) (h + g)}}} .}$

Kąt między cięciwami styczności k i l jest określony wzorem

${\ Displaystyle \ sin {\ varphi } = {\ sqrt {\ Frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+ h)(h+e)}}}.}$

Przekątne

Jeżeli e , f , g i h są długościami stycznymi od odpowiednio A , B , C i D do punktów , w których okrąg jest styczny do boków czworokąta stycznego ABCD , to długości przekątnych p = AC i q = BD są

${\displaystyle \displaystyle p={\sqrt {{\frac {e+g}{f+h}}{\duży (}(e+g)(f+h)+4fh{\duży }}}, }$

${\displaystyle \displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\duży (}(e+g)(f+h)+4eg {\duży }}}. }$

Akordy styczności

Jeżeli e , f , g i h są długościami stycznymi czworokąta stycznego, to długości pasów stycznych są

${\ Displaystyle \ Displaystyle k = {\ Frac {2 (efg + fgh + ghe + hef)} {\ sqrt {(e + f) (g + h) (e + g) (f + h)}}}, }$

${\ Displaystyle \ Displaystyle l = {\ Frac {2 (efg + fgh + ghe + hef)} {\ sqrt {(e + h) (f + g) (e + g) (f + h)}}}}$

gdzie pas styczności o długości k łączy boki o długościach a = e + f i c = g + h , a pas o długości l łączy boki o długościach b = f + g i d = h + e . Stosunek do kwadratu cięciw styczności spełnia

${\ Displaystyle {\ Frac {k ^ {2}} {l ^ {2}}} = {\ Frac {bd} {ac}}.}$

Dwa akordy styczne

• są prostopadłe wtedy i tylko wtedy, gdy styczne czworobok posiada również okrąg (to bicentric ).
• mieć równe długości wtedy i tylko wtedy, gdy czworokąt styczny jest latawcem .

Styczna cięciwa pomiędzy bokami AB i CD w stycznym czworoboku ABCD jest dłuższa niż ta pomiędzy bokami BC i DA wtedy i tylko wtedy, gdy bimediana pomiędzy bokami AB i CD jest krótsza niż pomiędzy bokami BC i DA .

Jeżeli styczny czworokąt ABCD ma punkty styczności W na AB i Y na CD , a cięciwa styczności WY przecina przekątną BD w punkcie M , to stosunek długości stycznych jest równy stosunkowi odcinków przekątnej BD . ${\ Displaystyle {\ tfrac {BW} {DY}}}$${\ Displaystyle {\ tfrac {BM} {DM}}}$

Punkty współliniowe

Jeżeli M ₁ i M ₂ są środkami przekątnych odpowiednio AC i BD w czworoboku stycznym ABCD o środku I , a pary przeciwległych boków spotykają się w J i K , gdzie M ₃ jest środkiem JK , to punkty M ₃ , M ₁ , I i M ₂ są współliniowe . Linia je zawierająca to linia Newtona czworokąta.

Jeżeli przedłużenia przeciwległych boków czworokąta stycznego przecinają się w J i K , a przedłużenia przeciwległych boków w czworoboku styku przecinają się w punktach L i M , to cztery punkty J , L , K i M są współliniowe.

Jeśli okrąg jest styczny do boków AB , BC , CD , DA w punktach odpowiednio T ₁ , T ₂ , T ₃ , T ₄ i jeśli N ₁ , N ₂ , N ₃ , N ₄ są sprzężeniami izotomicznymi tych punktów z stosunku do odpowiedniego boku (to jest w ₁ = BN ₁ i tak dalej), to punkt Nagel stycznego czworoboku jest określona jako przecięcie linii N ₁ N ₃ i N ₂ N ₄ . Obie te linie dzielą obwód czworoboku na dwie równe części. Co ważniejsze, punkt Nagela N , „centrum pola” G i środek I są w tej kolejności współliniowe, a NG = 2 GI . Ta linia nazywana jest linią Nagela stycznego czworoboku.

W stycznym czworoboku ABCD o środku I iw którym przecinają się przekątne w punkcie P , niech H _X , H _Y , H _Z , H _W będą ortośrodkami trójkątów AIB , BIC , CID , DIA . Wtedy punkty P , H _X , H _Y , H _Z , H _W są współliniowe.

Linie współbieżne i prostopadłe

Dwie przekątne i dwa cięciwy styczności są zbieżne . Jednym ze sposobów postrzegania tego jest przypadek graniczny twierdzenia Brianchona , które mówi, że sześciokąt, którego wszystkie boki są styczne do pojedynczej części stożkowej, ma trzy przekątne, które spotykają się w punkcie. Z czworoboku stycznego można utworzyć sześciokąt z dwoma kątami 180°, umieszczając dwa nowe wierzchołki w dwóch przeciwległych punktach styczności; wszystkie sześć boków tego sześciokąta leżą na liniach stycznych do wpisanego okręgu, więc jego przekątne spotykają się w punkcie. Ale dwie z tych przekątnych są takie same jak przekątne czworoboku stycznego, a trzecia przekątna sześciokąta jest linią przechodzącą przez dwa przeciwległe punkty styczności. Powtórzenie tego samego argumentu z pozostałymi dwoma punktami styczności uzupełnia dowód wyniku.

Jeżeli przedłużenia przeciwległych boków czworokąta stycznego przecinają się w J i K , a przekątne przecinają się w P , to JK jest prostopadłe do przedłużenia IP, gdzie I jest środkiem.

W centrum

Środek czworokąta stycznego leży na linii Newtona (łączącej punkty środkowe przekątnych).

Stosunek dwóch przeciwległych boków w czworoboku stycznym można wyrazić w postaci odległości między środkiem I a wierzchołkami zgodnie z

${\ Displaystyle {\ Frac {AB} {CD}} = {\ Frac {IA \ cdot IB} {IC \ cdot ID}}, \ quad \ quad {\ Frac {BC} {DA}} = {\ Frac { IB\cdot IC}{ID\cdot IA}}.}$

Iloczyn dwóch sąsiednich boków w stycznym czworoboku ABCD ze środkiem I spełnia

${\ Displaystyle AB \ cdot BC = IB ^ {2} + {\ Frac {IA \ cdot IB \ cdot IC} {ID}}.}$

Jeśli I jest środkiem stycznego czworokąta ABCD , to

${\ Displaystyle IA \ cdot IC + IB \ cdot ID = {\ sqrt {AB \ cdot BC \ cdot CD \ cdot DA}}.}$

Środek I w stycznym czworoboku ABCD pokrywa się z „centrum wierzchołków” czworokąta wtedy i tylko wtedy, gdy

${\ Displaystyle IA \ cdot IC = IB \ cdot ID.}$

Jeśli M _s i M _Q to środkowe przekątnych AC i BD odpowiednio stycznym czworokąt ABCD z incenter I , a następnie

${\ Displaystyle {\ Frac {IM_ {p}} {IM_ {q}}} = {\ Frac {IA \ cdot IC} {IB \ cdot ID}} = {\ Frac {e + g} {f + h} }}$

gdzie e , f , g i h są długościami stycznymi odpowiednio w punktach A , B , C i D . Łącząc pierwszą równość z poprzednią właściwością, „środek wierzchołka” czworoboku stycznego pokrywa się ze środkiem wtedy i tylko wtedy, gdy środek jest środkiem odcinka linii łączącego punkty środkowe przekątnych.

Jeśli połączenie czteroprętowe jest wykonane w postaci czworoboku stycznego, pozostanie ono styczne bez względu na to, jak połączenie jest zgięte, pod warunkiem, że czworokąt pozostaje wypukły. (Tak więc, na przykład, jeśli kwadrat jest zdeformowany w romb, pozostaje styczny, chociaż do mniejszego okręgu). Jeśli jedna strona jest utrzymywana w stałej pozycji, to gdy czworokąt jest zginany, środek tworzy okrąg o promieniu, gdzie a,b,c,d są bokami w kolejności, a s jest półobwodem. ${\displaystyle {\sqrt {abcd}}/s}$

Charakterystyki w czterech podtrójkątach

W nienakładających się trójkątach APB , BPC , CPD , DPA utworzonych przez przekątne czworokąta wypukłego ABCD , gdzie przecinają się przekątne w punkcie P , następuje charakterystyka czworokątów stycznych.

Niech R ₁ , R ₂ , r, ₃ i R ₄ oznaczają promienie incircles w czterech trójkątów APB , BPC , CPD i DPA, odpowiednio. Chao i Simeonov udowodnili, że czworokąt jest styczny wtedy i tylko wtedy, gdy

${\displaystyle {\frac {1}{r_{1}}}+{\frac{1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1 }{r_{4}}}.}$

Ta charakterystyka została udowodniona już pięć lat wcześniej przez Vaynshtejna. W rozwiązaniu jego problemu podobną charakterystykę podali Wasiljew i Senderow. Jeśli h ₁ , h ₂ , h ₃ i h ₄ oznaczają wysokości w tych samych czterech trójkątach (od przecięcia ukośnego do boków czworokąta), to czworokąt jest styczny wtedy i tylko wtedy, gdy

${\ Displaystyle {\ Frac {1} {h_ {1}}} + {\ Frac {1} {h_ {3}}} = {\ Frac {1} {h_ {2}}} + {\ Frac {1 }{h_{4}}}.}$

Kolejne podobne problemy CHARAKTERYSTYKA exradii R , R _b , R _c i R _d w tych samych czterech trójkątów (cztery excircles są styczne do siebie z boku w kształcie czworoboku i przedłużenie jego przekątnych). Czworokąt jest styczny wtedy i tylko wtedy, gdy

${\ Displaystyle {\ Frac {1} {r_ {a}}} + {\ Frac {1} {r_ {c}}} = {\ Frac {1} {r_ {b}}} + {\ Frac {1 }{r & D}}}.}$

Jeśli R ₁ , R ₂ , R ₃ i R ₄ oznaczają promienie w okręgach opisanych odpowiednio na trójkątach APB , BPC , CPD i DPA , to czworokąt ABCD jest styczny wtedy i tylko wtedy

${\displaystyle R_{1}+R_{3}=R_{2}+R_{4}.}$

W 1996 roku Vaynshtejn był prawdopodobnie pierwszym, który udowodnił kolejną piękną charakterystykę czworoboków stycznych, która później ukazała się w kilku czasopismach i witrynach internetowych. Stwierdza, że ​​gdy czworokąt wypukły jest podzielony na cztery nienakładające się trójkąty przez dwie przekątne, środki czterech trójkątów są koncykliczne wtedy i tylko wtedy, gdy czworokąt jest styczny. W rzeczywistości nakładki tworzą prostokątny cykliczny czworobok . Pokrewnym rezultatem jest to, że okręgi mogą być zamienione na eksokrąg do tych samych trójkątów (stycznych do boków czworoboku i przedłużeń jego przekątnych). Zatem czworokąt wypukły jest styczny wtedy i tylko wtedy, gdy mimośrody w tych czterech ekscentrach są wierzchołkami czworokąta cyklicznego .

Wypukły czworokąt ABCD , z przekątnymi przecinającymi się w punkcie P , jest styczny wtedy i tylko wtedy, gdy cztery mimośrody w trójkątach APB , BPC , CPD i DPA naprzeciw wierzchołków B i D są współcykliczne. Jeśli R , R _b , R _c i R _d są exradii w trójkątach APB , BPC , CPD i DPA odpowiednio naprzeciwko wierzchołków B i D , a następnym warunkiem, że czworobok jest styczna tylko wtedy, gdy

${\ Displaystyle {\ Frac {1} {R_ {a}}} + {\ Frac {1} {R_ {C}}} = {\ Frac {1} {R_ {b}}} + {\ Frac {1 }{R & D}}}.}$

Ponadto wypukły czworokąt ABCD z przekątnymi przecinającymi się w punkcie P jest styczny wtedy i tylko wtedy, gdy

${\ Displaystyle {\ Frac {a} {\ trójkąt (APB)}} + {\ Frac {c} {\ trójkąt (CPD)}} = {\ Frac {b} {\ trójkąt (BPC)}} + {\ frac {d}{\trójkąt (DPA)}}}$

gdzie ∆( APB ) jest polem trójkąta APB .

Oznacz odcinki, na które przekątna P dzieli przekątną AC jako AP = p ₁ i PC = p ₂ , i podobnie P dzieli przekątną BD na odcinki BP = q ₁ i PD = q ₂ . Wtedy czworokąt jest styczny wtedy i tylko wtedy, gdy którakolwiek z następujących równości jest prawdziwa:

${\displaystyle ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{2}+dp_{2}q_{1}}$

lub

${\displaystyle {\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_ {2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2 }+q_{1}+b)(p_{1}+q_{2}+d)}}}$

lub

${\displaystyle {\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c -p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_ {2}+q_{1})(d-p_{1}+q_{2})}}.}$

Warunki, aby czworokąt styczny był innym typem czworokąta

Romb

Styczny czworokąt jest rombem wtedy i tylko wtedy, gdy jego przeciwne kąty są równe.

latawiec

Styczny czworokąt to latawiec wtedy i tylko wtedy, gdy spełniony jest jeden z następujących warunków:

• Powierzchnia wynosi połowę iloczynu przekątnych .
• Przekątne są prostopadłe .
• Dwa odcinki linii łączące przeciwległe punkty styczności mają równe długości.
• Jedna para przeciwnych długości stycznych ma równe długości.
• W bimedians mają równe długości.
• Iloczyny przeciwnych stron są równe.
• Środek okręgu leży na przekątnej będącej osią symetrii.

Dwucentryczny czworobok

Jeśli okrąg jest styczny do boków AB , BC , CD , DA odpowiednio w W , X , Y , Z , to styczny czworokąt ABCD jest również cykliczny (a zatem dwucentryczny ) wtedy i tylko wtedy, gdy spełniony jest jeden z następujących warunków:

• WY jest prostopadły do XZ
• ${\ Displaystyle AW \ cdot CY = BW \ cdot DY}$
• ${\ Displaystyle {\ Frac {AC} {BD}} = {\ Frac {AW + CY} {BX + DZ}}}$

Pierwszy z tych trzech oznacza, że kontaktu czworoboku WXYZ jest orthodiagonal czworoboku .

Styczny czworokąt jest dwucentryczny wtedy i tylko wtedy, gdy jego promień jest większy niż jakikolwiek inny czworobok styczny o tej samej sekwencji długości boków.

Trapez styczny

Jeśli okrąg jest styczny do boków AB i CD odpowiednio w W i Y , to czworokąt styczny ABCD jest również trapezem o bokach równoległych AB i CD wtedy i tylko wtedy, gdy

${\ Displaystyle AW \ cdot DY = BW \ cdot CY}$

a AD i BC są równoległymi bokami trapezu wtedy i tylko wtedy, gdy

${\ Displaystyle AW \ cdot BW = CY \ cdot DY.}$

Zobacz też

• Zakreślony okrąg
• Czworobok ex-tangencjalny
• Trójkąt styczny
• Wielokąt styczny

Bibliografia

Linki zewnętrzne

• Weisstein, Eric W. , "Tangential Quadrilateral" , MathWorld