Równanie ciepła - Heat equation

Animowany wykres ewolucji temperatury na kwadratowej płycie metalowej zgodnie z przewidywaniami równania ciepła. Wysokość i zaczerwienienie wskazują temperaturę w każdym punkcie. Stan początkowy ma jednolicie gorący obszar w kształcie kopyta (czerwony) otoczony przez jednolicie zimny obszar (żółty). W miarę upływu czasu ciepło przenika do zimnego obszaru.

W matematyce i fizyce The równanie ciepła pewna częściowa równania różniczkowego . Rozwiązania równania ciepła są czasami nazywane funkcjami kalorycznymi . Teoria równania ciepła została po raz pierwszy opracowana przez Josepha Fouriera w 1822 roku w celu modelowania, w jaki sposób wielkość, taka jak ciepło, dyfunduje przez dany region.

Jako prototypowe paraboliczne równanie różniczkowe cząstkowe , równanie cieplne jest jednym z najszerzej badanych tematów w czystej matematyce , a jego analiza jest uważana za fundamentalną dla szerszej dziedziny równań różniczkowych cząstkowych . Równanie ciepła można również rozpatrywać na rozmaitościach riemannowskich , co prowadzi do wielu zastosowań geometrycznych. Podążając za pracą Subbaramiah Minakshisundarama i Åke Pleijela , równanie ciepła jest ściśle związane z geometrią spektralną . Przełomowy nieliniowy wariant równania ciepła został wprowadzony do geometrii różniczkowej przez Jamesa Eellsa i Josepha Sampsona w 1964 roku, inspirując wprowadzenie przepływu Ricciego przez Richarda Hamiltona w 1982 roku i którego kulminacją był dowód hipotezy Poincarégo autorstwa Grigori Perelmana w 2003 roku. rozwiązania równania cieplnego znanego jako jądra cieplne dostarczają subtelnych informacji o regionie, w którym są zdefiniowane, czego przykładem jest ich zastosowanie do twierdzenia o indeksie Atiyaha-Singera .

Równanie ciepła, wraz z jego wariantami, jest również ważne w wielu dziedzinach nauki i matematyki stosowanej . W teorii prawdopodobieństwa równanie ciepła jest połączone z badaniem losowych spacerów i ruchów Browna za pomocą równania Fokkera-Plancka . Black-Scholes równanie z matematyki finansowej jest mały wariant równania ciepła i równanie Schrödingera z mechaniki kwantowej można traktować jako równanie ciepła w czas urojony . W analizie obrazu równanie cieplne jest czasami używane do rozwiązywania pikselizacji i identyfikacji krawędzi . Po wprowadzeniu przez Roberta Richtmyera i Johna von Neumanna metod „sztucznej lepkości”, rozwiązania równań cieplnych były przydatne w matematycznym formułowaniu wstrząsów hydrodynamicznych . Rozwiązaniom równania cieplnego poświęcono również wiele uwagi w literaturze analitycznej , począwszy od lat 50. XX wieku w pracach Jima Douglasa, DW Peacemana i Henry'ego Rachforda Jr.

Stwierdzenie równania

W matematyce, jeśli dany podzbiór otwarty U od R ⁿ i podprzedział I od R , mówi się, że funkcja u  : U × I → R jest rozwiązaniem równania ciepła, jeśli

${\ Displaystyle {\ Frac {\ częściowy u} {\ częściowy t}} = {\ Frac {\ częściowy ^ {2} u} {\ częściowy x_ {1} ^ {2}}} + \ cdots + {\ Frac {\częściowy ^{2}u}{\częściowy x_{n}^{2}}},}$

gdzie ( x ₁ , …, x _n , t ) oznacza ogólny punkt dziedziny. Typowe jest odwoływanie się do t jako „czas”, a x ₁ , …, x _n do „zmiennych przestrzennych”, nawet w abstrakcyjnych kontekstach, w których te wyrażenia nie mają swojego intuicyjnego znaczenia. Zbiór zmiennych przestrzennych jest często nazywany po prostu x . Dla dowolnej danej wartości t , prawa strona równania jest Laplace'em funkcji u (⋅, t ): U → R . W związku z tym równanie ciepła jest często zapisywane bardziej zwięźle jako

W kontekście fizyki i inżynierii, zwłaszcza w kontekście dyfuzji przez medium, częściej ustala się kartezjański układ współrzędnych, a następnie rozważa szczególny przypadek funkcji u ( x , y , z , t ) trzech zmiennych przestrzennych ( x , y , z ) i zmienna czasowa t . Następnie mówi się, że u jest rozwiązaniem równania ciepła, jeśli

${\ Displaystyle {\ Frac {\ częściowy u}{\ częściowy t}} = \ alfa \ lewo ({\ Frac {\ częściowy ^ {2} u} {\ częściowy x ^ {2}}} + {\ Frac { \partial ^{2}u}{\częściowy y^{2}}}+{\frac {\partial ^{2}u}{\częściowy z^{2}}}\right)}$

gdzie α jest dodatnim współczynnikiem zwanym dyfuzyjnością cieplną ośrodka. Oprócz innych zjawisk fizycznych, równanie to opisuje przepływ ciepła w jednorodnym i izotropowym ośrodku, gdzie u ( x , y , z , t ) jest temperaturą w punkcie ( x , y , z ) i czasie t . Jeśli ośrodek nie jest jednorodny i izotropowy, to α nie będzie stałym współczynnikiem, lecz będzie zależeć od ( x , y , z ) ; równanie miałoby również nieco inną postać. W literaturze z zakresu fizyki i inżynierii powszechnie używa się ∇ ² do oznaczenia Laplace'a, a nie ∆ .

W matematyce, fizyce i technice powszechnie używa się notacji Newtona dla pochodnych czasowych, więc używa się go do oznaczenia${\ Displaystyle {\ kropka {u}}}$ u/t. Należy również zauważyć, że możliwość użycia ∆ lub ∇ ² do oznaczenia Laplace'a, bez wyraźnego odniesienia do zmiennych przestrzennych, jest odzwierciedleniem faktu, że Laplace'a jest niezależny od wyboru układu współrzędnych. W kategoriach matematycznych można by powiedzieć, że Laplace'a jest „niezmiennicza translacja i rotacja”. W rzeczywistości jest to (w dużym uproszczeniu) najprostszy operator różniczkowy, który ma te symetrie. Można to potraktować jako istotne (i czysto matematyczne) uzasadnienie użycia Laplace'a i równania ciepła do modelowania dowolnych zjawisk fizycznych, które są jednorodne i izotropowe, których głównym przykładem jest dyfuzja ciepła.

„Stała dyfuzyjności” α często nie występuje w matematycznych badaniach równania ciepła, podczas gdy jej wartość może być bardzo ważna w inżynierii. Nie jest to duża różnica z następującego powodu. Niech u będzie funkcją z

${\ Displaystyle {\ Frac {\ częściowy u}{\ częściowy t}} = \ alfa \ Delta u.}$

Zdefiniuj nową funkcję . Wtedy, zgodnie z zasadą łańcuszka , trzeba ${\ Displaystyle v (t, x) = u (t / \ alfa, x)}$

${\ Displaystyle {\ Frac {\ częściowy }{\ częściowy t}} v (t, x) = {\ Frac {\ częściowy} {\ częściowy t}} u (t / \ alfa, x) = \ alfa ^ { -1}{\frac {\częściowy u}{\częściowy t}}(t/\alfa ,x)=\Delta u(t/\alfa ,x)=\Delta v(t,x)}$

( ⁎ )

Istnieje więc prosty sposób tłumaczenia między rozwiązaniami równania ciepła o ogólnej wartości α a rozwiązaniami równania ciepła o α = 1 . W związku z tym, dla celów analizy matematycznej, często wystarczy rozważyć tylko przypadek α = 1 .

Ponieważ istnieje inna możliwość zdefiniowania satysfakcjonującego jak w ( ⁎ ) powyżej przez ustawienie . Należy zauważyć, że dwa możliwe sposoby definiowania omawianej tutaj nowej funkcji sprowadzają się, w kategoriach fizycznych, do zmiany jednostki miary czasu lub jednostki miary długości. ${\ Displaystyle \ alfa > 0}$${\displaystyle v}$${\textstyle {\frac {\częściowy }{\częściowy t}}v=\Delta v}$${\ Displaystyle v (t x) = u (t \ alfa ^ {-1/2} x)}$${\displaystyle v}$

Interpretacja

Fizyczna interpretacja równania

Nieformalnie operator Laplace'a ∆ podaje różnicę między średnią wartością funkcji w sąsiedztwie punktu, a jej wartością w tym punkcie. Tak więc, jeśli u jest temperaturą, ∆ mówi, czy (i o ile) materiał otaczający każdy punkt jest średnio cieplejszy lub zimniejszy niż materiał w tym punkcie.

Zgodnie z drugą zasadą termodynamiki ciepło będzie przepływać z ciał cieplejszych do sąsiednich ciał zimniejszych, proporcjonalnie do różnicy temperatur i przewodności cieplnej materiału między nimi. Gdy ciepło przepływa do (odpowiednio, z), z materiału, temperatura wzrasta (odpowiednio zmniejsza się) w stosunku do ilości ciepła, podzieloną przez ilość ( masy ) materiału, ze współczynnikiem proporcjonalności nazywa się zdolność ciepło z następujących materiał.

Dzięki połączeniu tych obserwacji równanie ciepła mówi, że szybkość, z jaką materiał w danym punkcie będzie się nagrzewać (lub schładzać) jest proporcjonalna do tego, o ile cieplejszy (lub chłodniejszy) jest otaczający materiał. Współczynnik α w równaniu uwzględnia przewodność cieplną, ciepło właściwe i gęstość materiału. ${\ Displaystyle {\ kropka {u}}}$

Matematyczna interpretacja równania

Pierwszą połowę powyższego myślenia fizycznego można przełożyć na formę matematyczną. Kluczem jest to, że dla dowolnego ustalonego x , trzeba

${\ Displaystyle {\ zacząć {wyrównany} u_ {(x)} (0) i = u (x) \ \ u_ {(x)} '(0) i = 0 \ \ u_ {(x)} ''( 0)&={\frac {1}{n}}\Delta u(x)\end{wyrównany}}}$

gdzie U _{( x )} ( R ) jest pojedynczym zmienną funkcją oznaczającą wartość średnią z U na powierzchni kuli o promieniu R środku w x ; może być zdefiniowany przez

${\ Displaystyle u_ {(x)} (r) = {\ Frac {1} {\ omega _ {n-1} r ^ {n-1}}} \ int _ {\ {y: | xy | = r \}}u\,d{\mathcal {H}}^{n-1},}$

gdzie ω _{n − 1} oznacza pole powierzchni kuli jednostkowej w n- wymiarowej przestrzeni euklidesowej. Formalizuje to powyższe stwierdzenie, że wartość ∆ u w punkcie x mierzy różnicę między wartością u ( x ) a wartością u w punktach w pobliżu x , w tym sensie, że ta ostatnia jest zakodowana przez wartości u _{( x )} ( r ) dla małych dodatnich wartości r .

Podążając za tą obserwacją, można interpretować równanie ciepła jako narzucające nieskończenie małe uśrednienie funkcji. Mając rozwiązanie równania ciepła, wartość u ( x , t + τ) dla małej dodatniej wartości τ można aproksymować jako1/2 nrazy średnią wartość funkcji u (⋅, t ) na kuli o bardzo małym promieniu, której środek znajduje się w punkcie x .

Charakter rozwiązań

Rozwiązanie równania różniczkowego cząstkowego ciepła 1D. Temperatura ( ) jest początkowo rozłożona w jednowymiarowym, jednojednostkowym przedziale ( x  = [0,1]) z izolowanymi punktami końcowymi. Rozkład zbliża się do równowagi w czasie.${\ Displaystyle u}$

Zachowanie temperatury, gdy boki pręta 1D mają stałą temperaturę (w tym przypadku 0,8 i 0 z początkowym rozkładem Gaussa). Temperatura zbliża się do funkcji liniowej, ponieważ jest to stabilne rozwiązanie równania: gdziekolwiek temperatura ma niezerową pochodną przestrzenną sekundy, pochodna czasowa również jest niezerowa.

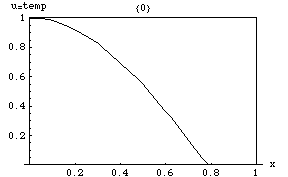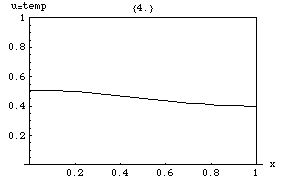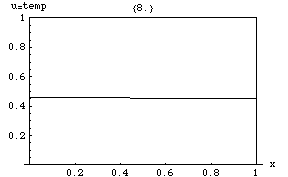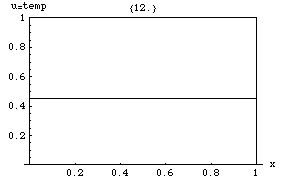
Z równania ciepła wynika, że ​​piki ( lokalne maksima ) będą stopniowo erodowane, a zagłębienia ( lokalne minima ) zostaną wypełnione. Wartość w pewnym momencie pozostanie stabilna tylko tak długo, jak będzie równa średniej wartości w jej bezpośrednim okolica. W szczególności, jeśli wartości w otoczeniu są bardzo zbliżone do funkcji liniowej , to wartość w środku tego otoczenia nie będzie się zmieniać w tym czasie (czyli pochodna będzie wynosić zero). ${\ Displaystyle u}$${\ Displaystyle Axe + Przez + Cz + D}$${\ Displaystyle {\ kropka {u}}}$

Bardziej subtelną konsekwencją jest zasada maksimum , która mówi , że maksymalna wartość w jakimkolwiek obszarze ośrodka nie przekroczy maksymalnej wartości , która wcześniej wystąpiła w , chyba że znajduje się na granicy . Oznacza to, że maksymalna temperatura w regionie może wzrosnąć tylko wtedy, gdy ciepło dociera z zewnątrz . Jest to właściwość parabolicznych równań różniczkowych cząstkowych i nie jest trudno ją udowodnić matematycznie (patrz poniżej). ${\ Displaystyle u}$${\ Displaystyle R}$${\ Displaystyle R}$${\ Displaystyle R}$${\ Displaystyle R}$${\ Displaystyle R}$

Inną interesującą właściwością jest to, że nawet jeśli początkowo ma ostry skok (nieciągłość) wartości na pewnej powierzchni wewnątrz ośrodka, skok ten jest natychmiast wygładzany przez chwilowe, nieskończenie krótkie, ale nieskończenie duże natężenie przepływu ciepła przez tę powierzchnię. Na przykład, jeśli dwa izolowane ciała, początkowo o jednakowych, ale różnych temperaturach i , zetkną się ze sobą, temperatura w punkcie kontaktu natychmiast przyjmie pewną wartość pośrednią, a wokół tego punktu rozwinie się strefa, w której będzie się stopniowo zmieniać między i . ${\ Displaystyle u}$${\displaystyle u_{0}}$${\displaystyle u_{1}}$${\ Displaystyle u}$${\displaystyle u_{0}}$${\displaystyle u_{1}}$

Jeśli pewna ilość ciepła zostanie nagle przyłożona do punktu w ośrodku, rozprzestrzeni się we wszystkich kierunkach w postaci fali dyfuzyjnej . W przeciwieństwie do fal sprężystych i elektromagnetycznych , prędkość fali dyfuzyjnej spada z czasem: w miarę rozprzestrzeniania się na większym obszarze gradient temperatury maleje, a zatem zmniejsza się również przepływ ciepła.

Konkretne przykłady

Przepływ ciepła w jednolitym pręcie

W przypadku przepływu ciepła równanie ciepła wynika z fizycznych praw przewodnictwa ciepła i zachowania energii ( Cannon 1984 ).

Zgodnie z prawem Fouriera dla ośrodka izotropowego, szybkość przepływu energii cieplnej na jednostkę powierzchni przez powierzchnię jest proporcjonalna do ujemnego gradientu temperatury na niej:

${\displaystyle \mathbf {q} =-k\\nabla u}$

gdzie jest przewodnością cieplną materiału, jest temperaturą i jest polem wektorowym, które reprezentuje wielkość i kierunek przepływu ciepła w punkcie czasoprzestrzennym . ${\displaystyle k}$${\displaystyle u=u(\mathbf {x},t)}$${\ Displaystyle \ mathbf {q} = \ mathbf {q} (\ mathbf {x}, t)}$${\displaystyle \mathbf {x}}$${\displaystyle t}$

Jeśli ośrodek jest cienkim prętem o jednolitym przekroju i materiale, pozycja jest pojedynczą współrzędną , przepływ ciepła w kierunku wzrostu jest polem skalarnym , a gradient jest zwykłą pochodną względem . Równanie staje się ${\displaystyle x}$${\displaystyle x}$${\displaystyle q=q(t,x)}$${\displaystyle x}$

${\displaystyle q=-k\{\frac {\częściowy u}{\częściowy x}}}$

Niech będzie wewnętrzną energią cieplną na jednostkę objętości pręta w każdym punkcie i czasie. W przypadku braku wytwarzania energii cieplnej ze źródeł zewnętrznych lub wewnętrznych, szybkość zmiany wewnętrznej energii cieplnej na jednostkę objętości materiału, , jest proporcjonalna do szybkości zmiany jego temperatury, . To jest, ${\ Displaystyle Q = Q (x, t)}$${\ Displaystyle \ częściowe Q/\ częściowe t}$${\ Displaystyle \ częściowe u/\ częściowe t}$

${\ Displaystyle {\ Frac {\ częściowy Q}{\ częściowy t}} = c\, \ rho \, {\ Frac {\ częściowy u}{\ częściowy t}}}$

gdzie jest właściwą pojemnością cieplną (przy stałym ciśnieniu, w przypadku gazu) i jest gęstością (masą na jednostkę objętości) materiału. To wyprowadzenie zakłada, że ​​materiał ma stałą gęstość masy i pojemność cieplną w przestrzeni i czasie. ${\displaystyle c}$${\ Displaystyle \ rho}$

Stosując zasadę zachowania energii na małym elemencie ośrodka o środku w , można dojść do wniosku, że szybkość akumulacji ciepła w danym punkcie jest równa zanegowanej pochodnej przepływu ciepła w tym punkcie. To jest, ${\displaystyle x}$${\displaystyle x}$

${\displaystyle {\frac {\częściowy Q}{\częściowy t}}=-{\frac {\częściowy q}{\częściowy x}}}$

Z powyższych równań wynika, że

${\displaystyle {\frac {\częściowy u}{\częściowy t}}\;=\;-{\frac {1}{c\rho}}{\frac {\częściowy q}{\częściowy x}}\ ;=\;-{\frac {1}{c\rho }}{\frac {\częściowy }{\częściowy x}}\left(-k\,{\frac {\częściowy u}{\częściowy x} }\right)\;=\;{\frac {k}{c\rho }}{\frac {\partial ^{2}u}{\częściowy x^{2}}}}$

czyli równanie ciepła w jednym wymiarze, ze współczynnikiem dyfuzyjności

${\ Displaystyle \ alfa = {\ Frac {k} {c \ rho}}}$

Ta wielkość nazywana jest dyfuzyjnością cieplną ośrodka.

Rachunkowość strat radiacyjnych

Do równania można wprowadzić dodatkowy człon, aby uwzględnić straty ciepła przez promieniowanie. Zgodnie z prawem Stefana–Boltzmanna terminem tym jest , gdzie jest temperaturą otoczenia i jest współczynnikiem zależnym od właściwości fizycznych materiału. Tempo zmian energii wewnętrznej staje się ${\ Displaystyle \ mu \ po lewej (u ^ {4}-v ^ {4} \ po prawej)}$${\displaystyle v=v(x,t)}$${\ Displaystyle \ mu}$

${\ Displaystyle {\ Frac {\ częściowy Q} {\ częściowy t}} = - {\ Frac {\ częściowy q} {\ częściowy x}} - \ mu \ lewo (u ^ {4}-v ^ {4} \Prawidłowy)}$

i równanie ewolucji staje się ${\ Displaystyle u}$

${\ Displaystyle {\ Frac {\ częściowy u}{\ częściowy t}} = {\ Frac {k} {c \ rho}} {\ Frac {\ częściowy ^ {2} u} {\ częściowy x ^ {2} }}-{\frac {\mu }{c\rho }}\left(u^{4}-v^{4}\right).}$

Niejednorodny ośrodek izotropowy

Zauważ, że równanie stanu, podane przez pierwszą zasadę termodynamiki (tj. zasada zachowania energii), jest zapisane w następującej postaci (zakładając brak transferu masy lub promieniowania). Ta forma jest bardziej ogólna i szczególnie przydatna do rozpoznawania, która właściwość (np. c _p lub ) wpływa na który termin. ${\ Displaystyle \ rho}$

${\ Displaystyle \ rho c_ {p} {\ Frac {\ częściowy T} {\ częściowy t}} - \ nabla \ cdot \ lewo (k \ nabla T \ po prawej) = {\ kropka {q}} _ {V} }$

gdzie jest wolumetryczne źródło ciepła. ${\ Displaystyle {\ kropka {q}} _ {V}}$

Problem trójwymiarowy

W szczególnych przypadkach propagacji ciepła w izotropowym i jednorodnym ośrodku w przestrzeni trójwymiarowej równanie to jest

${\ Displaystyle {\ Frac {\ częściowy u}{\ częściowy t}} = \ alfa \ nabla ^ {2} u = \ alfa \ lewo ({\ Frac {\ częściowy ^ {2} u} {\ częściowy x ^ {2}}}+{\frac {\częściowy ^{2}u}{\częściowy y^{2}}}+{\frac {\częściowy ^{2}u}{\częściowy z^{2}} }\Prawidłowy)}$   ${\ Displaystyle = \ alfa \ lewo (u_ {xx} + u_ {yy} + u_ {zz} \ po prawej)}$

gdzie:

• ${\displaystyle u=u(x,y,z,t)}$ jest temperaturą jako funkcją przestrzeni i czasu;
• ${\displaystyle {\tfrac {\częściowy u}{\częściowy t}}}$ jest szybkością zmian temperatury w pewnym momencie w czasie;
• ${\ Displaystyle u_ {xx}}$, Oraz są drugie przestrzenne pochodne ( conductions termiczne ) temperatury w , i kierunków, odpowiednio;${\displaystyle u_{rr}}$${\displaystyle u_{zz}}$${\displaystyle x}$${\displaystyle y}$${\displaystyle z}$
• ${\ Displaystyle \ alfa \ ekwiwalent {\ tfrac {k} {c_ {p} \ rho}}}$to dyfuzyjność cieplna , wielkość właściwa dla materiału zależna od przewodności cieplnej , właściwej pojemności cieplnej i gęstości masy .${\displaystyle k}$ ${\displaystyle c_{p}}$ ${\ Displaystyle \ rho}$

Równanie ciepła jest konsekwencją prawa przewodnictwa Fouriera (patrz przewodnictwo cieplne ).

Jeśli ośrodkiem nie jest cała przestrzeń, aby jednoznacznie rozwiązać równanie ciepła, musimy również określić warunki brzegowe dla u . Do określenia jednoznaczności rozwiązań w całej przestrzeni konieczne jest przyjęcie dodatkowych warunków, np. wiązania wykładniczego na wzroście rozwiązań lub warunku znaku (rozwiązania nieujemne są jednoznaczne dzięki wynikowi Davida Widdera ).

Rozwiązania równania ciepła charakteryzują się stopniowym wygładzaniem rozkładu temperatury początkowej przez przepływ ciepła z cieplejszych do zimniejszych obszarów obiektu. Ogólnie rzecz biorąc, wiele różnych stanów i warunków początkowych będzie dążyło do tej samej stabilnej równowagi . W konsekwencji odwrócenie rozwiązania i wnioskowanie o wcześniejszych czasach lub warunkach początkowych na podstawie obecnej dystrybucji ciepła jest bardzo niedokładne, z wyjątkiem najkrótszych okresów czasu.

Równanie ciepła jest prototypowym przykładem parabolicznego równania różniczkowego cząstkowego .

Za pomocą operatora Laplace'a równanie ciepła można uprościć i uogólnić na podobne równania w przestrzeniach o dowolnej liczbie wymiarów, jak

${\ Displaystyle u_ {t} = \ alfa \ nabla ^ {2} u = \ alfa \ Delta u}$

gdzie operator Laplace'a, Δ lub ∇ ² , rozbieżność gradientu, jest przyjmowany w zmiennych przestrzennych.

Równanie ciepła reguluje dyfuzję ciepła, a także inne procesy dyfuzyjne, takie jak dyfuzja cząstek lub propagacja potencjału czynnościowego w komórkach nerwowych. Chociaż nie mają one charakteru dyfuzyjnego, niektóre problemy mechaniki kwantowej są również regulowane przez matematyczny analog równania ciepła (patrz poniżej). Można go również wykorzystać do modelowania niektórych zjawisk zachodzących w finansach , takich jak procesy Blacka–Scholesa czy Ornsteina-Uhlenbecka . Równanie i różne nieliniowe analogi są również wykorzystywane w analizie obrazu.

Technicznie rzecz biorąc, równanie ciepła jest sprzeczne ze szczególną teorią względności , ponieważ jego rozwiązanie wiąże się z natychmiastową propagacją zakłócenia. Część zaburzenia poza przednim stożkiem światła można zwykle bezpiecznie pominąć, ale jeśli konieczne jest rozwinięcie rozsądnej prędkości przesyłania ciepła, należy zamiast tego rozważyć problem hiperboliczny – jak równanie różniczkowe cząstkowe z udziałem drugiego rzędu pochodna czasu. Niektóre modele nieliniowego przewodzenia ciepła (które są również równaniami parabolicznymi) mają rozwiązania ze skończoną prędkością transmisji ciepła.

Wewnętrzne wytwarzanie ciepła

Funkcja u powyżej reprezentuje temperaturę ciała. Alternatywnie, czasami wygodnie jest zmienić jednostki i przedstawić u jako gęstość ciepła ośrodka. Ponieważ gęstość ciepła jest proporcjonalna do temperatury w jednorodnym ośrodku, równanie ciepła jest nadal przestrzegane w nowych jednostkach.

Załóżmy, że ciało przestrzega równania ciepła, a ponadto wytwarza własne ciepło na jednostkę objętości (np. w watach/litr – W/L) z szybkością określoną przez znaną funkcję q, zmienną w czasie i przestrzeni. Wtedy ciepło na jednostkę objętości u spełnia równanie

${\ Displaystyle {\ Frac {1} {\ alfa}}{\ Frac {\ częściowy u}{\ częściowy t}} = \ lewo ({\ Frac {\ częściowy ^ {2} u} {\ częściowy x ^ { 2}}}+{\frac {\częściowy ^{2}u}{\częściowy y^{2}}}+{\frac {\częściowy ^{2}u}{\częściowy z^{2}}} \right)+{\frac {1}{k}}q.}$

Na przykład żarnik wolframowy generuje ciepło, więc po włączeniu będzie miał dodatnią, niezerową wartość dla q . Gdy światło jest wyłączone, wartość q dla żarnika wolframowego będzie wynosić zero.

Rozwiązywanie równania ciepła za pomocą szeregu Fouriera

Idealne ustawienie fizyczne dla przewodzenia ciepła w pręcie o jednorodnych warunkach brzegowych.

Poniższa technika rozwiązania równania ciepła została zaproponowana przez Josepha Fouriera w jego traktacie Théorie analytique de la chaleur , opublikowanym w 1822 roku. Rozważ równanie ciepła dla jednej zmiennej przestrzennej. Można to wykorzystać do modelowania przewodzenia ciepła w pręcie. Równanie to

${\ Displaystyle \ Displaystyle u_ {t} = \ alfa u_ {xx}}$

( 1 )

gdzie u = u ( x , t ) jest funkcją dwóch zmiennych x i t . Tutaj

• x jest zmienną przestrzenną, więc x ∈ [0, L ], gdzie L jest długością pręta.
• t jest zmienną czasu, więc t ≥ 0.

Zakładamy warunek początkowy

${\ Displaystyle u (x, 0) = f (x) \ quad \ dla wszystkich x \ w [0, L]}$

( 2 )

gdzie podana jest funkcja f i warunki brzegowe

${\ Displaystyle u (0, t) = 0 = u (L, t) \ quad \ forall t> 0}$.

( 3 )

Spróbujmy znaleźć rozwiązanie ( 1 ), które nie jest identycznie zerowe, spełniające warunki brzegowe ( 3 ), ale o następującej własności: u jest iloczynem, w którym rozdzielona jest zależność u od x , t , czyli:

${\ Displaystyle u (x, t) = X (x) T (t).}$

( 4 )

Ta technika rozwiązania nazywana jest separacją zmiennych . Podstawiając u z powrotem do równania ( 1 ),

${\ Displaystyle {\ Frac {T'(t)}{\ alfa T (t)}} = {\ Frac {X''(x)}{X (x)}}.}$

Ponieważ prawa strona zależy tylko od x, a lewa tylko od t , obie strony są równe pewnej stałej wartości −λ. Zatem:

${\ Displaystyle T '(t) = - \ lambda \ alfa T (t)}$

( 5 )

oraz

${\ Displaystyle X ''(x) = - \ lambda X (x).}$

( 6 )

Pokażemy teraz, że nietrywialne rozwiązania dla ( 6 ) dla wartości λ ≤ 0 nie mogą wystąpić:

1. Załóżmy, że λ < 0. Wtedy istnieją liczby rzeczywiste B , C takie, że
   $${\ Displaystyle X (x) = być ^ {{\ sqrt {-\ lambda}} \ x} + Ce ^ {- {\ sqrt {- \ lambda}} \ x}.}$$

   
   Z ( 3 ) otrzymujemy X (0) = 0 = X ( L ), a zatem B = 0 = C, co oznacza, że u jest identycznie równe 0.
2. Załóżmy, że λ = 0. Wtedy istnieją liczby rzeczywiste B , C takie , że X ( x ) = Bx + C . Z równania ( 3 ) wnioskujemy w taki sam sposób jak w 1, że u jest identycznie równe 0.
3. Dlatego musi być tak, że λ > 0. Wtedy istnieją liczby rzeczywiste A , B , C takie, że
   $${\ Displaystyle T (t) = Ae ^ {- \ lambda \ alfa t}}$$

   
   oraz
   $${\ Displaystyle X (x) = B \ sin \ lewo ({\ sqrt {\ lambda}} \, x \ prawo) + C \ cos \ lewo ({\ sqrt {\ lambda}}} \ x \ po prawej). }$$

   
   Z ( 3 ) otrzymujemy C = 0 i to dla pewnej dodatniej liczby całkowitej n ,
   $${\displaystyle {\sqrt {\lambda}}=n{\frac {\pi}{L}}.}$$

   

To rozwiązuje równanie ciepła w szczególnym przypadku, gdy zależność u ma specjalną postać ( 4 ).

Ogólnie rzecz biorąc, suma rozwiązań ( 1 ), które spełniają warunki brzegowe ( 3 ), również spełnia ( 1 ) i ( 3 ). Możemy pokazać, że rozwiązanie ( 1 ), ( 2 ) i ( 3 ) dane jest wzorem

${\ Displaystyle u (x, t) = \ suma _ {n = 1} ^ {\ infty} D_ {n} \ grzech \ lewo ({\ Frac {n \ pi x} {L}} \ po prawej) e ^ {-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}}$

gdzie

${\ Displaystyle D_ {n} = {\ Frac {2} {L}} \ int _ {0} ^ {L} f (x) \ grzech \ lewo ({\ Frac {n \ pi x} {l}} \prawo)\,dx.}$

Uogólnianie techniki rozwiązania

Zastosowaną powyżej technikę rozwiązywania można znacznie rozszerzyć na wiele innych typów równań. Pomysł polega na tym, że operator u _xx z zerowymi warunkami brzegowymi może być reprezentowany w kategoriach jego funkcji własnych . Prowadzi to naturalnie do jednej z podstawowych idei teorii spektralnej liniowych operatorów samosprzężonych .

Rozważmy operator liniowy Δ u = u _xx . Nieskończona sekwencja funkcji

${\ Displaystyle e_ {n} (x) = {\ sqrt {\ Frac {2} {L}}} \ grzech \ lewo ({\ Frac {n \ pi x} {L}} \ po prawej)}$

dla n ≥ 1 są funkcjami własnymi Δ. W rzeczy samej,

${\ Displaystyle \ Delta e_ {n} = - {\ Frac {n ^ {2} \ pi ^ {2}} {L ^ {2}}} e_ {n}.}$

Ponadto każda funkcja własna f z Δ z warunkami brzegowymi f (0) = f ( L ) = 0 ma postać e _n dla pewnego n ≥ 1. Funkcje e _n dla n ≥ 1 tworzą ciąg ortonormalny względem pewien iloczyn skalarny na przestrzeni funkcji rzeczywistych na [0, L ]. To znaczy

${\ Displaystyle \ langle e_ {n} e_ {m} \ rangle = \ int _ {0} ^ {L} e_ {n} (x) e_ {m} ^ {*} (x) dx = \ delta _ {m.}}$

Wreszcie, sekwencja { e _n } _{n ∈ N} obejmuje gęstą liniową podprzestrzeń L ² ((0, L )). To pokazuje, że w efekcie przekątowaliśmy operator Δ.

Przewodzenie ciepła w niejednorodnych ośrodkach anizotropowych

Ogólnie rzecz biorąc, badanie przewodzenia ciepła opiera się na kilku zasadach. Przepływ ciepła jest formą przepływu energii i jako taki można mówić o szybkości przepływu ciepła w danym obszarze przestrzeni.

• Szybkość przepływu ciepła do obszaru V jest określona przez zależną od czasu wielkość q _t ( V ). Zakładamy, że q ma gęstość Q , więc
  $${\ Displaystyle q_ {t} (V) = \ int _ {V} Q (x, t) \ dx \ quad}$$

  
• Przepływ ciepła jest zależną od czasu funkcją wektorową H ( x ) charakteryzującą się następująco: szybkość przepływu ciepła przez nieskończenie mały element powierzchniowy o polu dS i jednostkowym wektorze normalnym n wynosi
  $${\ Displaystyle \ mathbf {H} (x) \ cdot \ mathbf {n} (x) \ dS.}$$

  
  Zatem szybkość przepływu ciepła do V jest również podana przez całkę powierzchniową
  $${\ Displaystyle q_ {t} (V) = - \ int _ {\ częściowy V} \ mathbf {H} (x) \ cdot \ mathbf {n} (x) \ dS}$$

  
  gdzie n ( x ) jest skierowanym na zewnątrz wektorem normalnym w punkcie x .
• Prawo Fouriera mówi, że przepływ energii cieplnej ma następującą zależność liniową od gradientu temperatury
  $${\ Displaystyle \ mathbf {H} (x) = - \ mathbf {A} (x) \ cdot \ nabla u (x)}$$

  
  gdzie A ( x ) jest macierzą rzeczywistą 3 × 3 , która jest symetryczna i dodatnio określona .
• Zgodnie z twierdzeniem o dywergencji poprzednia całka powierzchniowa dla przepływu ciepła w V może być przekształcona w całkę objętościową
  $${\ Displaystyle {\ zacząć {wyrównany} q_ {t} (V) & = - \ int _ {\ częściowy V} \ mathbf {H} (x) \ cdot \ mathbf {n} (x) \ dS \ \ &=\int _{\częściowe V}\mathbf {A} (x)\cdot \nabla u(x)\cdot \mathbf {n} (x)\,dS\\&=\int _{V}\ suma _{i,j}\częściowa _{x_{i}}{\bigl (}a_{ij}(x)\częściowa _{x_{j}}u(x,t){\bigr )}\, dx\end{wyrównany}}}$$

  
• Szybkość zmiany temperatury w punkcie x jest proporcjonalna do ciepła przepływającego do elementu o nieskończenie małej objętości, gdzie stała proporcjonalności zależy od stałej κ
  $${\ Displaystyle \ częściowy _ {t} u (x, t) = \ kappa (x) Q (x, t)}$$

  

Zestawienie tych równań razem daje ogólne równanie przepływu ciepła:

${\ Displaystyle \ częściowy _ {t} u (x, t) = \ kappa (x) \ suma _ {i, j} \ częściowy _ {x_ {i}} {\ bigl (} a_ {ij} (x) \częściowa _{x_{j}}u(x,t){\bigr )}}$

Uwagi .

• Współczynnik κ ( x ) oznacza odwrotność wartości ciepła w substancji na X x gęstości substancji w x : .${\ Displaystyle \ kappa = 1/(\ rho c_ {p})}$
• W przypadku ośrodka izotropowego matryca A jest matrycą skalarną równą przewodności cieplnej k .
• W przypadku anizotropowym, gdy macierz współczynników A nie jest skalarna i/lub zależy od x , rzadko można zapisać jednoznaczny wzór na rozwiązanie równania ciepła, chociaż zwykle można rozważyć związany z nim abstrakcyjny problem Cauchy'ego i pokazać, że jest to dobrze postawiony problem i/lub pokazać pewne właściwości jakościowe (takie jak zachowanie pozytywnych danych początkowych, nieskończona prędkość propagacji, zbieżność w kierunku równowagi, właściwości wygładzania). Zwykle robi się to za pomocą teorii półgrup jednoparametrowych : na przykład, jeśli A jest macierzą symetryczną, to operator eliptyczny zdefiniowany przez
  $${\ Displaystyle Au (x): = \ suma _ {i, j} \ częściowa _ {x_ {i}} a_ {ij} (x) \ częściowa _ {x_ {j}} u (x)}$$

  
  jest samosprzężona i rozpraszalna, a zatem na podstawie twierdzenia spektralnego generuje jednoparametrową półgrupę .

Podstawowe rozwiązania

Rozwiązaniem podstawowym , zwanym także jądrem ciepła , jest rozwiązanie równania ciepła odpowiadającego początkowemu stanowi punktowego źródła ciepła w znanej pozycji. Można je wykorzystać do znalezienia ogólnego rozwiązania równania ciepła w pewnych dziedzinach; zob. na przykład ( Evans 2010 ), aby zapoznać się z wstępnym leczeniem.

W jednej zmiennej funkcja Greena jest rozwiązaniem problemu wartości początkowej (zgodnie z zasadą Duhamela , równoważną definicji funkcji Greena jako jednej z funkcją delta jako rozwiązaniem pierwszego równania)

${\ Displaystyle {\ zacząć {przypadki} u_ {t} (x, t) -ku_ {xx} (x, t) = 0 i (x, t) \ w \ mathbb {R} \ razy (0, \ infty) \\u(x,0)=\delta (x)&\end{przypadki}}}$

gdzie δ jest funkcją delta Diraca . Rozwiązaniem tego problemu jest rozwiązanie podstawowe ( jądro ciepła )

${\ Displaystyle \ Phi (x, t) = {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ exp \ lewo (- {\ Frac {x ^ {2}} {4 kt}} \ prawej ).}$

Można uzyskać ogólne rozwiązanie jednozmiennego równania ciepła z warunkiem początkowym u ( x , 0 ) = g ( x ) dla −∞ < x < ∞ i 0 < t < ∞ przez zastosowanie splotu :

${\ Displaystyle u (x, t) = \ int \ Phi (xy, t) g (y) dy.}$

W kilku zmiennych przestrzennych rozwiązanie podstawowe rozwiązuje analogiczny problem

${\ Displaystyle {\ zacząć {przypadki} u_ {t} (\ mathbf {x}, t)-k \ suma _ {i = 1} ^ {n} u_ {x_ {i} x_ {i}} (\ mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \mathbb {R} ^{n}\times (0,\infty )\\u(\mathbf {x} ,0)=\ delta (\mathbf {x} )\end{przypadki}}}$

Rozwiązanie podstawowe dla n zmiennej jest iloczynem rozwiązań podstawowych w każdej zmiennej; tj,

${\ Displaystyle \ Phi (\ mathbf {x}, t) = \ Phi (x_ {1}, t) \ Phi (x_ {2}, t) \ cdots \ Phi (x_ {n}, t) = {\ frac {1}{\sqrt {(4\pi kt)^{n}}}}\exp \left(-{\frac {\mathbf {x} \cdot \mathbf {x} }{4kt}}\right ).}$

Ogólne rozwiązanie równania ciepła na R ⁿ jest następnie otrzymywane przez splot, tak że aby rozwiązać problem z wartością początkową z u ( x , 0) = g ( x ), trzeba

${\ Displaystyle u (\ mathbf {x} t) = \ int _ {\ mathbb {R} ^ {n}} \ Phi (\ mathbf {x} - \ mathbf {y}, t) g (\ mathbf { y} )d\mathbf {y} .}$

Ogólny problem w dziedzinie Ω w R ⁿ to

${\ Displaystyle {\ zacząć {przypadki} u_ {t} (\ mathbf {x}, t)-k \ suma _ {i = 1} ^ {n} u_ {x_ {i} x_ {i}} (\ mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \Omega \times (0,\infty )\\u(\mathbf {x} ,0)=g(\mathbf {x} ) &\mathbf {x} \w \Omega \end{cases}}}$

z danymi granicznymi Dirichleta lub Neumanna . Funkcja Greena zawsze istnieje, ale o ile dziedzinę Ω nie da się łatwo rozłożyć na problemy z jedną zmienną (patrz poniżej), może nie być możliwe jej wyraźne zapisanie. Inne metody uzyskiwania funkcji Greena obejmują metodę obrazów , separację zmiennych i przekształcenia Laplace'a (Cole, 2011).

Niektóre rozwiązania funkcji Greena w 1D

Zapisano tutaj wiele podstawowych rozwiązań funkcjonalnych Greena w jednym wymiarze; wiele innych jest dostępnych gdzie indziej. W niektórych z nich domeną przestrzenną jest (−∞,∞). W innych jest to półnieskończony przedział (0,∞) z warunkami brzegowymi Neumanna lub Dirichleta . Kolejną wariacją jest to, że niektóre z nich rozwiązują niejednorodne równanie

${\ Displaystyle u_ {t} = ku_ {xx} + f.}$

gdzie f jest określoną funkcją x i t .

Jednorodne równanie ciepła

Zagadnienie wartości początkowej na (−∞,∞)

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} i (x, t) \ w \ mathbb {R} \ razy (0, \ infty) \ \ u (x, 0) = g ( x)&{\text{Warunek początkowy}}\end{przypadki}}}$

${\ Displaystyle u (x, t) = {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ int _ {- \ infty} ^ {\ infty} \ exp \ lewo (- {\ Frac { (xy)^{2}}{4kt}}\prawo)g(y)\,dy}$

Podstawowe rozwiązanie jednowymiarowego równania ciepła. Czerwony: przebieg czasu . Niebieski: przebiegi czasowe dla dwóch wybranych punktów x ₀ = 0,2 i x ₀ = 1. Zwróć uwagę na różne czasy narastania/opóźnienia i amplitudy. Wersja interaktywna.${\ Displaystyle \ Phi (x, t)}$${\ Displaystyle \ Phi (x_ {0}, t)}$

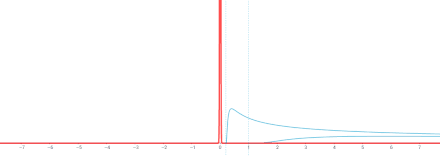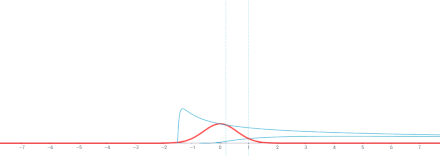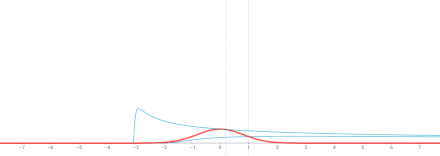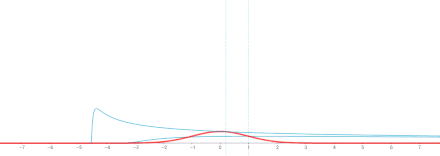
Komentarz . To rozwiązanie jest splotem względem zmiennej x rozwiązania podstawowego

${\ Displaystyle \ Phi (x, t): = {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ exp \ lewo (- {\ Frac {x ^ {2}} {4 kt}} \ Prawidłowy),}$

oraz funkcja g ( x ). ( Numer funkcji Greena rozwiązania podstawowego to X00.)

Dlatego, zgodnie z ogólnymi właściwościami splotu w odniesieniu do różniczkowania, u = g ∗ Φ jest rozwiązaniem tego samego równania cieplnego, dla

${\ Displaystyle \ lewo (\ częściowy _ {t} - k \ częściowy _ {x} ^ {2} \ prawej) (\ Phi * g) = \ lewo [\ lewo (\ częściowy _ {t} - k \ częściowy _{x}^{2}\prawo)\Phi \prawo]*g=0.}$

Ponadto,

${\ Displaystyle \ Phi (x, t) = {\ Frac {1} {\ sqrt {t}}} \ \ Phi \ lewo ({\ Frac {x} {\ sqrt {t}}}, 1 \ prawo )}$

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} \ Phi (x, t) \ dx = 1,}$

tak, że przez ogólne fakty dotyczące aproksymacji do tożsamości , Φ(⋅, t ) ∗ g → g jako t → 0 w różnych znaczeniach, zgodnie z konkretnym g . Na przykład, jeśli założymy , że g jest ograniczone i ciągłe na R, wtedy Φ(⋅, t ) ∗ g zbiega się jednostajnie do g jako t → 0, co oznacza, że u ( x , t ) jest ciągłe na R × [0, ∞) z u ( x , 0) = g ( x ).

Zagadnienie wartości początkowej na (0,∞) z jednorodnymi warunkami brzegowymi Dirichleta

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} i (x, t) \ w [0, \ infty) \ razy (0, \ infty) \ \ u (x, 0) = g (x)&{\text{IC}}\\u(0,t)=0&{\text{BC}}\end{przypadki}}}$

${\ Displaystyle u (x, t) = {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ int _ {0} ^ {\ infty} \ lewo [\ exp \ lewo (- {\ Frac {(xy)^{2}}{4kt}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y )\,dy}$

Komentarz. To rozwiązanie otrzymuje się z poprzedniego wzoru zastosowanego do danych g ( x ) odpowiednio rozszerzonych do R , tak aby była funkcją nieparzystą , to znaczy, przyjmując g ( −x ):=− g ( x ) dla wszystkich x . Odpowiednio, rozwiązanie problemu wartości początkowej na (−∞,∞) jest funkcją nieparzystą względem zmiennej x dla wszystkich wartości t , a w szczególności spełnia jednorodne warunki brzegowe Dirichleta u (0, t ) = 0 . na numer Greena funkcji tego rozwiązania jest X10.

Zagadnienie wartości początkowej na (0,∞) z jednorodnymi warunkami brzegowymi Neumanna

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} i (x, t) \ w [0, \ infty) \ razy (0, \ infty) \ \ u (x, 0) = g (x)&{\text{IC}}\\u_{x}(0,t)=0&{\text{BC}}\end{przypadki}}}$

${\ Displaystyle u (x, t) = {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ int _ {0} ^ {\ infty} \ lewo [\ exp \ lewo (- {\ Frac {(xy)^{2}}{4kt}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4kt}}\right)\right]g(y )\,dy}$

Komentarz. To rozwiązanie otrzymuje się z pierwszego wzoru rozwiązania zastosowanego do danych g ( x ) odpowiednio rozszerzonych do R tak, aby była funkcją parzystą , to znaczy, pozwalając g ( −x ) := g ( x ) dla wszystkich x . Odpowiednio, rozwiązanie problemu wartości początkowej R jest funkcją parzystą względem zmiennej x, dla wszystkich wartości t > 0, w szczególności, jest gładka, to spełnia jednorodne Neumann warunków brzegowych u _x (0, t ) = 0. Numer funkcji Greena tego rozwiązania to X20.

Problem na (0,∞) z jednorodnymi warunkami początkowymi i niejednorodnymi warunkami brzegowymi Dirichleta

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} i (x, t) \ w [0, \ infty) \ razy (0, \ infty) \ \ u (x, 0) = 0 i {\text{IC}}\\u(0,t)=h(t)&{\text{BC}}\end{przypadki}}}$

${\ Displaystyle u (x, t) = \ int _ {0} ^ {t} {\ Frac {x} {\ sqrt {4 \ pi k (ts) ^ {3}}}} \ exp \ lewo (- {\frac {x^{2}}{4k(ts)}}\right)h(s)\,ds,\qquad \forall x>0}$

Komentarz . To rozwiązanie jest splotem względem zmiennej t z

${\ Displaystyle \ psi (x, t): = -2 k \ częściowy _ {x} \ Phi (x, t) = {\ Frac {x} {\ sqrt {4 \ pi kt ^ {3}}}} \ exp \left(-{\frac {x^{2}}{4kt}}\right)}$

oraz funkcję h ( t ). Ponieważ Φ( x , t ) jest podstawowym rozwiązaniem

${\ Displaystyle \ częściowy _ {t}-k \ częściowy _ {x} ^ {2}}$

funkcja ψ ( x, t ) jest również rozwiązaniem tego samego równania cieplnego, podobnie jak u  := ψ ∗ h , dzięki ogólnym własnościom splotu względem różniczkowania. Ponadto,

${\ Displaystyle \ psi (x, t) = {\ Frac {1} {x ^ {2}}} \ \ psi \ lewo (1, {\ Frac {t} {x ^ {2}}} \ prawej )}$

${\ Displaystyle \ int _ {0} ^ {\ infty} \ psi (x, t) \ dt = 1,}$

tak więc, przez ogólne fakty dotyczące aproksymacji do tożsamości , ψ ( x , ⋅) ∗ h → h jako x → 0 w różnych znaczeniach, zgodnie z konkretnym h . Na przykład, jeśli założymy , że h jest ciągłe na R z podparciem w [0, ∞), to ψ ( x , ⋅) ∗ h zbiega się jednostajnie na compacta do h jako x → 0, co oznacza, że u ( x, t ) jest ciągłe na [ 0, ∞) × [0, ∞) z u (0, t ) = h ( t ).

Przedstawiono numeryczne rozwiązanie niejednorodnego równania ciepła. Równanie zostało rozwiązane przy zerowych warunkach początkowych i brzegowych oraz wyrazie źródłowym reprezentującym palnik na kuchence.

Niejednorodne równanie ciepła

Problem na (-∞,∞) jednorodnych warunkach początkowych

Komentarz . To rozwiązanie jest splotem w R ² , to znaczy w odniesieniu do obu zmiennych x i t , rozwiązania podstawowego

${\ Displaystyle \ Phi (x, t): = {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ exp \ lewo (- {\ Frac {x ^ {2}} {4 kt}} \ Prawidłowy)}$

oraz funkcję f ( x, t ), obie oznaczane jako zdefiniowane na całym R ² i identycznie 0 dla wszystkich t → 0. Weryfikuje się, że

${\ Displaystyle \ lewo (\ częściowy _ {t} - k \ częściowy _ {x} ^ {2} \ prawej) (\ Phi * F) = f}$

co wyrażone w języku dystrybucji staje się

${\ Displaystyle \ lewo (\ częściowy _ {t}-k \ częściowy _ {x} ^ {2} \ prawej) \ Phi = \ delta,}$

gdzie rozkład δ jest funkcją delta Diraca , czyli wartością 0.

Problem na (0,∞) z jednorodnymi warunkami brzegowymi Dirichleta i warunkami początkowymi

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} + f (x, t) i (x, t) \ w [0, \ infty) \ razy (0, \ infty) \ \ u (x,0)=0&{\text{IC}}\\u(0,t)=0&{\text{BC}}\end{przypadki}}}$

${\ Displaystyle u (x, t) = \ int _ {0} ^ {t} \ int _ {0} ^ {\ infty} {\ Frac {1} {\ sqrt {4 \ pi k (ts)}} }\left(\exp \left(-{\frac {(xy)^{2}}{4k(ts)}}\right)-\exp \left(-{\frac {(x+y)^{ 2}}{4k(ts)}}\prawo)\prawo)f(y,s)\,dy\,ds}$

Komentarz . To rozwiązanie otrzymuje się z poprzedniego wzoru zastosowanego do danych f ( x , t ) odpowiednio rozszerzonych do R × [0,∞), tak aby było nieparzystą funkcją zmiennej x , to znaczy, pozwalając f (− x , t ) := − f ( x , t ) dla wszystkich x i t . Odpowiednio, rozwiązanie niejednorodnego problemu na (−∞,∞) jest funkcją nieparzystą względem zmiennej x dla wszystkich wartości t , a w szczególności spełnia jednorodne warunki brzegowe Dirichleta u (0, t ) = 0.

Problem na (0,∞) z jednorodnymi warunkami brzegowymi Neumanna i warunkami początkowymi

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} + f (x, t) i (x, t) \ w [0, \ infty) \ razy (0, \ infty) \ \ u (x,0)=0&{\text{IC}}\\u_{x}(0,t)=0&{\text{BC}}\end{cases}}}$

${\ Displaystyle u (x, t) = \ int _ {0} ^ {t} \ int _ {0} ^ {\ infty} {\ Frac {1} {\ sqrt {4 \ pi k (ts)}} }\left(\exp \left(-{\frac {(xy)^{2}}{4k(ts)}}\right)+\exp \left(-{\frac {(x+y)^{ 2}}{4k(ts)}}\prawo)\prawo)f(y,s)\,dy\,ds}$

Komentarz . To rozwiązanie jest otrzymywane z pierwszego wzoru zastosowanego do danych f ( x , t ) odpowiednio rozszerzonych do R × [0,∞), tak aby było parzystą funkcją zmiennej x , to znaczy niech f (− x , t ) := f ( x , t ) dla wszystkich x i t . Odpowiednio, rozwiązanie tego problemu w niejednorodnym (-∞, ∞) jest również funkcją stosunku do zmiennej x, dla wszystkich wartości T , w szczególności, będąc gładką funkcji, spełnia jednorodne Neumann warunków brzegowych u _x ( 0, t ) = 0.

Przykłady

Ponieważ równanie ciepła jest liniowe, rozwiązania innych kombinacji warunków brzegowych, członu niejednorodnego i warunków początkowych można znaleźć, biorąc odpowiednią kombinację liniową powyższych rozwiązań funkcji Greena.

Na przykład, aby rozwiązać

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} + f i (x, t) \ w \ mathbb {R} \ razy (0, \ infty) \ \ u (x, 0) = g (x)&{\text{IC}}\end{przypadki}}}$

niech u = w + v gdzie w i v rozwiążą problemy

${\ Displaystyle {\ zacząć {przypadki} v_ {t} = kv_ {xx} + f \, w_ {t} = kW_ {xx} \ & (x, t) \ w \ mathbb {R} \ razy ( 0,\infty )\\v(x,0)=0,\,w(x,0)=g(x)\,&{\text{IC}}\end{cases}}}$

Podobnie do rozwiązania

${\ Displaystyle {\ zacząć {przypadki} u_ {t} = ku_ {xx} + f i (x, t) \ w [0, \ infty) \ razy (0, \ infty) \ \ u (x, 0) = g(x)&{\text{IC}}\\u(0,t)=h(t)&{\text{BC}}\end{przypadki}}}$

niech u = w + v + r gdzie w , v i r rozwiążą zadania

${\ Displaystyle {\ zacząć {przypadki} v_ {t} = kv_ {xx} + f, \, w_ {t} = kw_ {xx}, \, r_ {t} = kr_ {xx} i (x, t) \in [0,\infty )\times (0,\infty )\\v(x,0)=0,\;w(x,0)=g(x),\;r(x,0)= 0&{\text{IC}}\\v(0,t)=0,\;w(0,t)=0,\;r(0,t)=h(t)&{\text{BC} }\end{przypadki}}}$

Właściwość wartości średniej dla równania ciepła

Rozwiązania równań cieplnych

${\ Displaystyle (\ częściowy _ {t} - \ Delta) u = 0}$

spełniają własności średniowartościowe analogiczne do własności średniowartościowych funkcji harmonicznych , rozwiązania

${\ Displaystyle \ Delta u = 0,}$

choć nieco bardziej skomplikowane. Dokładniej, jeśli u rozwiązuje

${\ Displaystyle (\ częściowy _ {t} - \ Delta) u = 0}$

oraz

${\ Displaystyle (x, t) + E_ {\ lambda} \ podzbiór \ operatorname {dom} (u)}$

następnie

${\ Displaystyle u (x, t) = {\ Frac {\ lambda} {4}} \ int _ {E_ {\ lambda}} u (xy, ts) {\ Frac {| y | ^ {2}} s^{2}}}ds\,dy,}$

gdzie E _λ jest „kulą cieplną”, czyli nadpoziomowym zbiorem podstawowego rozwiązania równania cieplnego:

${\ Displaystyle E_ {\ lambda}: = \ {(y, s): \ Phi (y, s)> \ lambda \},}$

${\ Displaystyle \ Phi (x, t): = (4t \ pi) ^ {- {\ Frac {n} {2}}} \ exp \ lewo (- {\ Frac {| x | ^ {2}}} 4t}}\prawo).}$

Zauważ, że

${\ Displaystyle \ operatorname {diam} (E_ {\ lambda}) = o (1)}$

jako λ → ∞ więc powyższy wzór obowiązuje dla dowolnego ( x, t ) w (otwartym) zbiorze dom( u ) dla λ wystarczająco dużego. Można to wykazać za pomocą argumentu podobnego do analogicznego dla funkcji harmonicznych .

Równanie ciepła w stanie ustalonym

Równanie ciepła w stanie ustalonym z definicji nie jest zależne od czasu. Innymi słowy, zakłada się istnienie takich warunków, że:

${\displaystyle {\frac {\częściowy u}{\częściowy t}}=0}$

Warunek ten zależy od stałej czasowej i czasu, jaki upłynął od nałożenia warunków brzegowych. Warunek ten jest więc spełniony w sytuacjach, w których stała równowagi czasu jest na tyle szybka, że bardziej złożone, zależne od czasu równanie ciepła może być aproksymowane przez przypadek stanu ustalonego. Równoważnie stan ustalony istnieje we wszystkich przypadkach, w których minęło wystarczająco dużo czasu, aby pole cieplne u już nie ewoluowało w czasie.

W przypadku stanu ustalonego przestrzenny gradient termiczny może (lub nie) istnieć, ale jeśli tak, to nie zmienia się w czasie. To równanie opisuje zatem końcowy wynik wszystkich problemów termicznych, w których źródło jest włączone (na przykład silnik uruchomiony w samochodzie) i minęło wystarczająco dużo czasu, aby wszystkie stałe gradienty temperatury ustabilizowały się w przestrzeni, po czym te przestrzenne Gradienty nie zmieniają się już w czasie (podobnie jak w przypadku samochodu, w którym silnik pracował wystarczająco długo). Drugim (trywialnym) rozwiązaniem jest zniknięcie wszystkich gradientów temperatury przestrzennej, w którym to przypadku temperatura staje się również jednolita w przestrzeni.

Równanie jest znacznie prostsze i może pomóc w lepszym zrozumieniu fizyki materiałów bez skupiania się na dynamice procesu transportu ciepła. Jest szeroko stosowany w prostych zadaniach inżynierskich, przy założeniu, że w czasie istnieje równowaga pól temperatury i transportu ciepła.

Stan stacjonarny:

${\displaystyle {\frac {\częściowy u}{\częściowy t}}=0}$

Równanie ciepła w stanie ustalonym dla objętości zawierającej źródło ciepła (przypadek niejednorodny) to równanie Poissona :

${\displaystyle -k\nabla ^{2}u=q}$

gdzie u jest temperaturą , k jest przewodnością cieplną, a q gęstością strumienia ciepła źródła.

W elektrostatyce jest to równoznaczne z przypadkiem, w którym rozważana przestrzeń zawiera ładunek elektryczny.

Równanie ciepła w stanie ustalonym bez źródła ciepła w objętości (przypadek jednorodny) jest równaniem w elektrostatyce dla objętości wolnej przestrzeni, która nie zawiera ładunku. Opisuje to równanie Laplace'a :

${\ Displaystyle \ nabla ^ {2} u = 0}$

Aplikacje

Dyfuzja cząstek

Można modelować cząstek dyfuzji przez równanie udziałem albo:

• stężenie objętościowe cząstek, oznaczone c , w przypadku kolektywnej dyfuzji dużej liczby cząstek, lub
• funkcja gęstości związane z położeniem pojedynczej cząstki, oznaczona P .

W obu przypadkach używa się równania ciepła

${\ Displaystyle C_ {t} = D \ Delta C}$

lub

${\ Displaystyle P_ {t} = D \ Delta P.}$

Zarówno c, jak i P są funkcjami pozycji i czasu. D jest współczynnikiem dyfuzji, który kontroluje prędkość procesu dyfuzji i jest zwykle wyrażany w metrach do kwadratu na sekundę. Jeżeli współczynnik dyfuzji D nie jest stały, ale zależy od stężenia c (lub P w drugim przypadku), otrzymujemy nieliniowe równanie dyfuzji .

Ruch Browna

Niech proces stochastyczny będzie rozwiązaniem stochastycznego równania różniczkowego${\ Displaystyle X}$

${\ Displaystyle {\ zacząć {przypadki} \ operator {d} X_ {t} = {\ sqrt {2 k}} \; \ operatorname {d} B_ {t} \ \ X_ {0} = 0 \ koniec {przypadki} }}$

gdzie jest proces Wienera (standardowy ruch Browna). Następnie funkcja gęstości od podaje się w dowolnym czasie przez ${\ Displaystyle B}$${\ Displaystyle X}$${\displaystyle t}$

${\ Displaystyle {\ Frac {1} {\ sqrt {4 \ pi kt}}} \ exp \ po lewej (- {\ Frac {x ^ {2}} {4 kt}} \ po prawej)}$

co jest rozwiązaniem problemu z wartością początkową

${\ Displaystyle {\ rozpocząć {przypadki} u_ {t} (x, t)-ku_ {xx} (x, t) = 0 i (x, t) \ w \ mathbb {R} \ razy (0, + \infty )\\u(x,0)=\delta (x)\end{cases}}}$

gdzie jest funkcja delta Diraca . ${\ Displaystyle \ delta}$

Równanie Schrödingera dla cząstki swobodnej

Za pomocą prostego podziału równanie Schrödingera dla pojedynczej cząstki o masie m przy braku przyłożonego pola siłowego można przepisać w następujący sposób:

${\ Displaystyle \ psi _ {t} = {\ Frac {i \ hbar} {2 m}} \ Delta \ psi}$,

gdzie i jest jednostką urojoną , ħ jest zredukowaną stałą Plancka , a ψ jest funkcją falową cząstki.

To równanie jest formalnie podobne do równania dyfuzji cząstek, które otrzymuje się poprzez następującą transformację:

${\ Displaystyle {\ zacząć {wyrównany} c (\ mathbf {R} t) i \ psi (\ mathbf {R} t) \ \ D i \ do {\ Frac {i \ hbar} {2 m}} \end{wyrównany}}}$

Zastosowanie tej transformacji do wyrażeń funkcji Greena wyznaczonych w przypadku dyfuzji cząstek daje funkcje Greena równania Schrödingera , które z kolei można wykorzystać do uzyskania funkcji falowej w dowolnym momencie poprzez całkę z funkcji falowej przy t = 0:

${\ Displaystyle \ psi (\ mathbf {R} t) = \ int \ psi \ lewo (\ mathbf {R} ^ {0}, t = 0 \ prawo) G \ lewo (\ mathbf {R} - \ mathbf {R} ^{0},t\right)dR_{x}^{0}\,dR_{y}^{0}\,dR_{z}^{0},}$

z

${\ Displaystyle G (\ mathbf {R}, t) = \ lewo ({\ Frac {m} {2 \ pi i \ hbar t}} \ prawej) ^ {3/2} e ^ {- {\ Frac { \mathbf {R} ^{2}m}{2i\hbar t}}}.}$

Uwaga: ta analogia między mechaniką kwantową a dyfuzją ma charakter czysto formalny. Fizycznie ewolucja funkcji falowej spełniająca równanie Schrödingera może mieć inne pochodzenie niż dyfuzja.

Dyfuzyjność cieplna w polimerach

Bezpośrednie praktyczne zastosowanie równania ciepła, w związku z teorią Fouriera w sferycznych współrzędnych jest przewidywanie profili transferu termicznego i pomiar współczynnika dyfuzji cieplnej w polimerach (Unsworth i Duarte ). Ta podwójna metoda teoretyczno-eksperymentalna ma zastosowanie do gumy, różnych innych materiałów polimerowych o znaczeniu praktycznym i mikropłynów. Autorzy ci wyprowadzili wyrażenie na temperaturę w środku kuli T _C

${\ Displaystyle {\ Frac {T_ {C}-T_ {S}} {T_ {0}-T_ {S}}} = 2 \ suma _ {n = 1} ^ {\ infty} (-1) ^ { n+1}\exp \left({-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}\right)}$

gdzie T ₀ jest temperaturą początkową kuli, a T _S temperaturą na powierzchni kuli o promieniu L . Równanie to znalazło również zastosowanie w transferze energii białek i modelowaniu termicznym w biofizyce.

Dalsze zastosowania

Równanie ciepła pojawia się w modelowaniu szeregu zjawisk i jest często wykorzystywane w matematyce finansowej do modelowania opcji . The Black Scholes opcji cen modelu równanie różniczkowe mogą być przekształcone do równania ciepła umożliwiający stosunkowo łatwe rozwiązań ze znanego korpusu matematyki. Wiele rozszerzeń prostych modeli opcji nie ma rozwiązań formy zamkniętej i dlatego należy je rozwiązać numerycznie, aby uzyskać modelowaną cenę opcji. Równanie opisujące dyfuzję ciśnienia w ośrodku porowatym ma postać identyczną z równaniem ciepła. Problemy dyfuzji dotyczące warunków brzegowych Dirichleta , Neumanna i Robina mają zamkniętą formę rozwiązań analitycznych ( Thambynayagam 2011 ). Równanie cieplne jest również szeroko stosowane w analizie obrazu ( Perona i Malik 1990 ) oraz w uczeniu maszynowym jako teoria napędzająca metody Laplace'a w przestrzeni skali lub grafu . Równanie ciepła można skutecznie rozwiązać numerycznie przy użyciu niejawnej metody Crank-Nicolson ( Crank i Nicolson 1947 ). Metoda ta może być rozszerzona na wiele modeli bez rozwiązania formy zamkniętej, patrz na przykład ( Wilmott, Howison i Dewynne 1995 ).

Abstrakcyjna forma równania ciepła na rozmaitościach zapewnia główne podejście do twierdzenia o indeksie Atiyaha-Singera i doprowadziła do znacznie dalszych prac nad równaniami ciepła w geometrii riemannowskiej .

Zobacz też

• Wielomian kaloryczny
• Przepływ skracający krzywą
• Równanie dyfuzji
• Relatywistyczne przewodzenie ciepła
• Równanie Schrödingera
• Przekształcenie Weierstrassa

Uwagi

Bibliografia

• Korba, J.; Nicolson, P. (1947), „Praktyczna metoda oceny numerycznej rozwiązań równań różniczkowych cząstkowych typu przewodnictwa cieplnego”, Proceedings of the Cambridge Philosophical Society , 43 (1): 50-67, Bibcode : 1947PCPS .. .43...50C , doi : 10.1017/S0305004100023197
• Einstein, Albert (1905), "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen", Annalen der Physik , 322 (8): 549-560, Bibcode : 1905AnP...322..549E , doi : 10.1002/andp.19053220806
• Thambynayagam, RKM (2011), The Diffusion Handbook: Applied Solutions for Engineers , McGraw-Hill Professional, ISBN 978-0-07-175184-1
• Perona, P; Malik, J. (1990), "Scale-Space and Edge Detection Using Anisotropic Diffusion" (PDF) , IEEE Transactions on Pattern Analysis and Machine Intelligence , 12 (7): 629-639, doi : 10.1109/34.56205
• Unsworth, J.; Duarte, FJ (1979), „Dyfuzja ciepła w stałej sferze i teoria Fouriera”, Am. J. Fiz. , 47 (11): 891–893, Bibcode : 1979AmJPh..47..981U , doi : 10.1119/1.11601

Podręczniki

• Cannon, John Rozier (1984), Jednowymiarowe równanie ciepła , Encyklopedia matematyki i jej zastosowania, 23 , Czytanie, MA: Addison-Wesley Publishing Company, Advanced Book Program, ISBN 0-201-13522-1, MR  0747979 , Zbl  0567.35001
• Carslaw, HS ; Jaeger, JC (1988), Przewodzenie ciepła w ciałach stałych , Oxford Science Publications (2nd ed.), New York: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853368-9
• Cole, Kevin D.; Beck, James V.; Hadżi-Szejk, A.; Litkouhi, Bahan (2011), Przewodzenie ciepła za pomocą funkcji Greena , Seria w procesach obliczeniowych i fizycznych w mechanice i naukach cieplnych (2nd ed.), Boca Raton, FL: CRC Press, ISBN 978-1-43-981354-6
• Evans, Lawrence C. (2010), Równania różniczkowe cząstkowe , Graduate Studies in Mathematics, 19 (2nd ed.), Providence, RI: American Mathematical Society, ISBN 978-0-8218-4974-3
• Friedman, Avner (1964), Równania różniczkowe cząstkowe typu parabolicznego , Englewood Cliffs, NJ: Prentice-Hall, Inc.
• John Fritz (1991), Równania różniczkowe cząstkowe (4 wyd.), New York: Springer-Verlag, ISBN 978-0-387-90609-6
• Widder, DV (1975), równanie ciepła , matematyka czysta i stosowana, 67 , New York-London: Academic Press [Harcourt Brace Jovanovich, Publishers]
• Wilmott, Paweł; Howison, Sam; Dewynne, Jeff (1995), Matematyka pochodnych instrumentów finansowych. Wprowadzenie dla studentów , Cambridge: Cambridge University Press, ISBN 0-521-49699-3

Zewnętrzne linki

• Wyprowadzenie równania ciepła
• Liniowe równania cieplne : Rozwiązania szczegółowe i zagadnienia brzegowe - z EqWorld
• „Równanie ciepła” . Seria nieskończona PBS . 17 listopada 2017 – przez YouTube .