Przestrzeń (matematyka) - Space (mathematics)

W matematyce , o przestrzeń jest zestaw (czasami nazywany wszechświat ) z niektórymi dodaje struktury .

Chociaż nowoczesne matematyka używa wielu rodzajów pomieszczeń, takich jak euklidesowych , przestrzenie liniowe , przestrzeni topologicznych , przestrzenie Hilberta lub spacjami prawdopodobieństwa , to nie definiuje pojęcia „przestrzeni” sama.

Pomieszczenie składa się z wybranych obiektów matematycznych, które są traktowane jako punkty, oraz wybranych relacji między tymi punktami. Charakter punktów może być bardzo różny: na przykład punkty mogą być elementami zbioru, funkcjami w innej przestrzeni lub podprzestrzeniami innej przestrzeni. To relacje określają charakter przestrzeni. Dokładniej, przestrzenie izomorficzne są uważane za identyczne, gdzie izomorfizm między dwiema przestrzeniami jest korespondencją jeden do jednego między ich punktami, która zachowuje relacje. Na przykład relacje między punktami trójwymiarowej przestrzeni euklidesowej są jednoznacznie określone przez aksjomaty Euklidesa, a wszystkie trójwymiarowe przestrzenie euklidesowe są uważane za identyczne.

Pojęcia topologiczne, takie jak ciągłość, mają naturalne definicje w każdej przestrzeni euklidesowej. Jednak topologia nie rozróżnia linii prostych od krzywych, a zatem relacja między przestrzenią euklidesową a przestrzenią topologiczną jest „zapominająca”. Tego rodzaju relacje szerzej omówiono w rozdziale „Typy przestrzeni” .

Nie zawsze jest jasne, czy dany obiekt matematyczny należy traktować jako geometryczną „przestrzeń”, czy jako „strukturę” algebraiczną. Ogólna definicja „struktury”, zaproponowana przez Bourbakiego , obejmuje wszystkie powszechne typy przestrzeni, podaje ogólną definicję izomorfizmu i uzasadnia przenoszenie własności pomiędzy strukturami izomorficznymi.

Historia

Tabela 1 | Historyczny rozwój pojęć matematycznych

Klasyczny	Nowoczesny
aksjomaty są oczywistymi implikacjami definicji	aksjomaty są konwencjonalne
twierdzenia są absolutną obiektywną prawdą	twierdzenia są implikacjami odpowiednich aksjomatów
relacje między punktami, liniami itp. są zdeterminowane ich naturą	istotne są relacje między punktami, liniami itp.; ich natura nie jest
Obiekty matematyczne są nam dane wraz z ich strukturą	każda teoria matematyczna opisuje swoje obiekty za pomocą niektórych ich właściwości
geometria odpowiada rzeczywistości eksperymentalnej	geometria to prawda matematyczna
wszystkie właściwości geometryczne przestrzeni wynikają z aksjomatów	aksjomaty przestrzeni nie muszą określać wszystkich własności geometrycznych
geometria jest autonomiczną i żywą nauką	geometria klasyczna to uniwersalny język matematyki
przestrzeń jest trójwymiarowa	różne koncepcje wymiarów mają zastosowanie do różnych rodzajów przestrzeni
przestrzeń jest wszechświatem geometrii	przestrzenie to tylko struktury matematyczne, występują w różnych gałęziach matematyki

Przed złotym wiekiem geometrii

W matematyce starożytnej Grecji „przestrzeń” była geometryczną abstrakcją trójwymiarowej rzeczywistości obserwowanej w życiu codziennym. Około 300 pne Euklides podał aksjomaty dla własności przestrzeni. Euclid zbudował całą matematykę na tych geometrycznych podstawach, posuwając się nawet do definiowania liczb przez porównanie długości odcinków linii z długością wybranego odcinka odniesienia.

Metodę współrzędnych ( geometrię analityczną ) przyjął René Descartes w 1637 roku. W tym czasie twierdzenia geometryczne były traktowane jako absolutne obiektywne prawdy poznawalne intuicją i rozumem, podobne do przedmiotów nauk przyrodniczych; a aksjomaty były traktowane jako oczywiste implikacje definicji.

Wykorzystano dwie relacje równoważności między figurami geometrycznymi: zgodność i podobieństwo . Przekłady, rotacje i odbicia przekształcają figurę w przystające figury; homotheties — na podobne liczby. Na przykład wszystkie okręgi są do siebie podobne, ale elipsy nie są podobne do okręgów. Trzecia relacja równoważności, wprowadzona przez Gasparda Monge w 1795, występuje w geometrii rzutowej : nie tylko elipsy, ale także parabole i hiperbole zamieniają się w okręgi pod wpływem odpowiednich przekształceń rzutowych; wszystkie są projekcyjnie równoważnymi liczbami.

Relacja między dwiema geometriami, euklidesową i rzutową, pokazuje, że obiekty matematyczne nie są nam dane wraz z ich strukturą . Raczej każda teoria matematyczna opisuje swoje obiekty przez niektóre ich właściwości, dokładnie te, które są stawiane jako aksjomaty u podstaw teorii.

Odległości i kąty nie mogą występować w twierdzeniach geometrii rzutowej, ponieważ pojęcia te nie są ani wymieniane w aksjomatach geometrii rzutowej, ani definiowane z wymienionych tam pojęć. Pytanie „jaka jest suma trzech kątów trójkąta” ma sens w geometrii euklidesowej, ale nie ma sensu w geometrii rzutowej.

Odmienna sytuacja pojawiła się w XIX wieku: w niektórych geometriach suma trzech kątów trójkąta jest dobrze określona, ​​ale różni się od wartości klasycznej (180 stopni). Nieeuklidesowa hiperboliczny geometrii , wprowadzony przez Nikolai Lobachevsky w 1829 i János Bolyai w 1832 roku (i Carl Friedrich Gauss w 1816, niepublikowany) stwierdził, że suma zależy od trójkąta i jest zawsze mniejszy niż 180 stopni. Eugenio Beltrami w 1868 i Felix Klein w 1871 uzyskali euklidesowe „modele” nieeuklidesowej geometrii hiperbolicznej i tym samym całkowicie uzasadnili tę teorię jako logiczną możliwość.

Odkrycie to wymusiło porzucenie pretensji do absolutnej prawdy geometrii euklidesowej. Pokazał, że aksjomaty nie są „oczywiste”, ani „implikacje definicji”. Są to raczej hipotezy. W jakim stopniu odpowiadają rzeczywistości eksperymentalnej? Ten ważny problem fizyczny nie ma już nic wspólnego z matematyką. Nawet jeśli „geometria” nie odpowiada rzeczywistości eksperymentalnej, jej twierdzenia pozostają nie mniej „prawdami matematycznymi”.

Euklidesowy model geometrii nieeuklidesowej to wybór niektórych obiektów istniejących w przestrzeni euklidesowej i pewnych relacji między tymi obiektami, które spełniają wszystkie aksjomaty (a zatem wszystkie twierdzenia) geometrii nieeuklidesowej. Te euklidesowe obiekty i relacje „grają” nieeuklidesową geometrię, jak współcześni aktorzy grający starożytne przedstawienie. Aktorzy potrafią naśladować sytuację, która nigdy nie miała miejsca w rzeczywistości. Relacje między aktorami na scenie imitują relacje między postaciami w sztuce. Podobnie wybrane relacje pomiędzy wybranymi obiektami modelu euklidesowego imitują relacje nieeuklidesowe. Pokazuje, że relacje między obiektami są istotne w matematyce, podczas gdy natura obiektów nie.

Złoty wiek i później

Słowo „geometria” (od starożytnego greckiego: geo- „ziemia”, -metron „pomiar”) początkowo oznaczało praktyczny sposób przetwarzania długości, regionów i objętości w przestrzeni, w której żyjemy, ale później zostało szeroko rozszerzone (także jako pojęcie przestrzeni, o której tu mowa).

Według Bourbaki, okres od 1795 ( Géométrie opisujący Monge) do 1872 ( "program Erlangen" Kleina) można nazwać złotym wiekiem geometrii. Pierwotna przestrzeń badana przez Euklidesa jest teraz nazywana trójwymiarową przestrzenią euklidesową . Jego dzana, rozpoczęty przez Euklidesa 23 wieków temu, został zreformowany z Aksjomatyka Hilberta , aksjomaty Tarskiego i aksjomatów Birkhoffa . Te systemy aksjomatów opisują przestrzeń za pomocą pojęć pierwotnych (takich jak „punkt”, „pomiędzy”, „przystający”), ograniczonych przez szereg aksjomatów .

Geometria analityczna poczyniła ogromne postępy i z powodzeniem zastąpiła twierdzenia geometrii klasycznej obliczeniami za pomocą niezmienników grup transformacji. Od tego czasu nowe twierdzenia geometrii klasycznej są bardziej interesujące dla amatorów niż dla zawodowych matematyków. Jednak dziedzictwo klasycznej geometrii nie zostało utracone. Według Bourbaki, „pominięta w roli autonomicznej i żywej nauki, geometria klasyczna zostaje w ten sposób przemieniona w uniwersalny język współczesnej matematyki”.

Jednocześnie liczby zaczęły wypierać geometrię jako podstawę matematyki. Na przykład Richard Dedekind w eseju Stetigkeit und irraationale Zahlen z 1872 r. ( Ciągłość i liczby niewymierne ) twierdzi, że punkty na prostej powinny mieć właściwości cięć Dedekinda , a zatem prosta jest tym samym, co zbiór liczb rzeczywistych. . Dedekind uważa, że ​​jest to założenie, którego nie można udowodnić. We współczesnym leczeniu twierdzenie Dedekinda jest często uważane za definicję linii, redukując w ten sposób geometrię do arytmetyki. Trójwymiarowa przestrzeń euklidesowa jest definiowana jako przestrzeń afiniczna, której powiązana przestrzeń wektorowa różnic jej elementów jest wyposażona w iloczyn skalarny. Definicja „od zera”, jak u Euklidesa, nie jest obecnie często używana, ponieważ nie ujawnia relacji tej przestrzeni do innych przestrzeni. Również trójwymiarowa przestrzeń rzutowa jest teraz definiowana jako przestrzeń wszystkich jednowymiarowych podprzestrzeni (czyli linii prostych przechodzących przez początek) czterowymiarowej przestrzeni wektorowej. Ta zmiana podstaw wymaga nowego zestawu aksjomatów, a jeśli te aksjomaty zostaną przyjęte, klasyczne aksjomaty geometrii stają się twierdzeniami.

Przestrzeń składa się teraz z wybranych obiektów matematycznych (na przykład funkcji w innej przestrzeni lub podprzestrzeni innej przestrzeni lub po prostu elementów zbioru) traktowanych jako punkty i wybranych relacji między tymi punktami. Dlatego przestrzenie są tylko wygodnymi strukturami matematycznymi. Można się spodziewać, że struktury zwane „przestrzeniami” są postrzegane bardziej geometrycznie niż inne obiekty matematyczne, ale nie zawsze jest to prawdą.

Zgodnie ze słynnym wykładem inauguracyjnym wygłoszonym przez Bernharda Riemanna w 1854 roku, każdy obiekt matematyczny sparametryzowany n liczbami rzeczywistymi może być traktowany jako punkt w n- wymiarowej przestrzeni wszystkich takich obiektów. Współcześni matematycy rutynowo podążają za tą ideą i uważają za niezwykle sugestywne niemal wszędzie posługiwanie się terminologią geometrii klasycznej.

Funkcje są ważnymi obiektami matematycznymi. Zwykle tworzą one nieskończenie wymiarowe przestrzenie funkcyjne , jak zauważył już Riemann i rozwinął w XX wieku analizę funkcjonalną .

Taksonomia przestrzeni

Trzy szeregi taksonomiczne

Chociaż każdy rodzaj przestrzeni ma swoją własną definicję, ogólna idea „przestrzeni” wymyka się formalizacji. Niektóre struktury nazywa się przestrzeniami, inne nie, bez formalnego kryterium. Co więcej, nie ma zgody co do ogólnej idei „struktury”. Według Pudláka „Matematyka [...] nie może być całkowicie wyjaśniona jednym pojęciem, takim jak struktura matematyczna. Niemniej jednak strukturalistyczne podejście Bourbaki jest najlepsze, jakie mamy”. Powrócimy do strukturalnego podejścia Bourbakiego w ostatniej części „Przestrzenie i struktury”, podczas gdy teraz nakreślimy możliwą klasyfikację przestrzeni (i struktur) w duchu Bourbakiego.

Klasyfikujemy przestrzenie na trzech poziomach. Biorąc pod uwagę, że każda teoria matematyczna opisuje swoje obiekty za pomocą niektórych ich właściwości, pierwsze pytanie, które należy zadać, brzmi: które właściwości? Prowadzi to do pierwszego (górnego) poziomu klasyfikacji. Na drugim poziomie brane są pod uwagę odpowiedzi na szczególnie ważne pytania (wśród pytań, które mają sens na poziomie pierwszym). Na trzecim poziomie klasyfikacji uwzględnia się odpowiedzi na wszystkie możliwe pytania.

Na przykład klasyfikacja wyższego poziomu rozróżnia przestrzenie euklidesowe i rzutowe , ponieważ odległość między dwoma punktami jest zdefiniowana w przestrzeniach euklidesowych, ale niezdefiniowana w przestrzeniach rzutowych. Inny przykład. Pytanie "jaka jest suma trzech kątów trójkąta" ma sens w przestrzeni euklidesowej, ale nie w przestrzeni rzutowej. W przestrzeni nieeuklidesowej pytanie ma sens, ale odpowiedź jest inna, co nie jest rozróżnieniem wyższego poziomu.

Również rozróżnienie między płaszczyzną euklidesową a trójwymiarową przestrzenią euklidesową nie jest rozróżnieniem wyższego poziomu; pytanie „jaki jest wymiar” ma sens w obu przypadkach.

Klasyfikacja drugiego poziomu rozróżnia na przykład przestrzenie euklidesowe i nieeuklidesowe; między przestrzeniami skończenie wymiarowymi i nieskończenie wymiarowymi; między przestrzeniami zwartymi i niezwartymi itp. W terminologii Bourbaki'ego klasyfikacja drugiego poziomu to klasyfikacja według „gatunków”. W przeciwieństwie do taksonomii biologicznej, przestrzeń może należeć do kilku gatunków.

Klasyfikacja trzeciego poziomu rozróżnia np. przestrzenie o różnych wymiarach, ale nie rozróżnia płaszczyzny trójwymiarowej przestrzeni euklidesowej, traktowanej jako dwuwymiarowa przestrzeń euklidesowa, od zbioru wszystkich par liczb rzeczywistych, traktowany również jako dwuwymiarowa przestrzeń euklidesowa. Podobnie nie rozróżnia między różnymi modelami euklidesowymi tej samej przestrzeni nieeuklidesowej. Bardziej formalnie, trzeci poziom klasyfikuje przestrzenie do izomorfizmu . Izomorfizm między dwiema przestrzeniami jest definiowany jako korespondencja jeden-do-jednego między punktami pierwszej przestrzeni a punktami drugiej przestrzeni, która zachowuje wszystkie relacje ustalone na poziomie pierwszym. Wzajemnie izomorficzne przestrzenie są uważane za kopie pojedynczej przestrzeni. Jeśli jeden z nich należy do danego gatunku, to wszystkie.

Pojęcie izomorfizmu rzuca światło na klasyfikację wyższego poziomu. Mając przyporządkowanie jeden do jednego między dwiema przestrzeniami tej samej klasy wyższego poziomu, można zapytać, czy jest to izomorfizm, czy nie. To pytanie nie ma sensu dla dwóch przestrzeni różnych klas.

Izomorfizm sam w sobie nazywa się automorfizmem. Automorfizmy przestrzeni euklidesowej to przesunięcia, obroty, odbicia i ich kompozycje. Przestrzeń euklidesowa jest jednorodna w tym sensie, że każdy punkt może zostać przekształcony w każdy inny punkt przez jakiś automorfizm.

Aksjomaty Euklidesa nie pozostawiają wolności; określają jednoznacznie wszystkie właściwości geometryczne przestrzeni. Dokładniej: wszystkie trójwymiarowe przestrzenie euklidesowe są wzajemnie izomorficzne. W tym sensie mamy do czynienia z trójwymiarową przestrzenią euklidesową. W terminologii Bourbaki, odpowiednia teoria jest jednowartościowa . Natomiast przestrzenie topologiczne są na ogół nieizomorficzne; ich teoria jest wielowartościowa . Podobna idea pojawia się w logice matematycznej: teorię nazywa się kategoryczną, jeśli wszystkie jej modele tej samej kardynalności są wzajemnie izomorficzne. Według Bourbaki, badanie teorii wielowartościowych jest najbardziej uderzającą cechą, która odróżnia matematykę współczesną od matematyki klasycznej.

Relacje między gatunkami przestrzeni

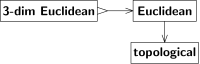
Pojęcia topologiczne (ciągłość, zbieżność, zbiory otwarte, zbiory domknięte itp.) są definiowane w sposób naturalny w każdej przestrzeni euklidesowej. Innymi słowy, każda przestrzeń euklidesowa jest również przestrzenią topologiczną. Każdy izomorfizm między dwiema przestrzeniami euklidesowymi jest również izomorfizmem między odpowiadającymi mu przestrzeniami topologicznymi (zwanymi „ homeomorfizmem ”), ale jest odwrotnie: homeomorfizm może zniekształcać odległości. W terminologii Bourbaki „przestrzeń topologiczna” jest strukturą leżącą u podstaw struktury „przestrzeni euklidesowej”. Podobne idee pojawiają się w teorii kategorii : kategoria przestrzeni euklidesowych jest kategorią konkretną ponad kategorią przestrzeni topologicznych; zapominalskich (lub „stripping”) funktor odwzorowuje dawną kategorię do tej drugiej kategorii.

Trójwymiarowa przestrzeń euklidesowa jest szczególnym przypadkiem przestrzeni euklidesowej. W terminologii Bourbakiego gatunek trójwymiarowej przestrzeni euklidesowej jest bogatszy niż gatunek przestrzeni euklidesowej. Podobnie gatunki o zwartej przestrzeni topologicznej są bogatsze niż gatunki o przestrzeni topologicznej.

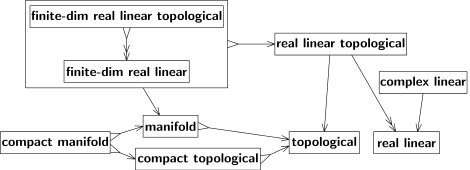
Takie relacje między gatunkami przestrzeni można wyrazić schematycznie, jak pokazano na rys. 3. Strzałka od A do B oznacza, że ​​każda przestrzeń A jest również przestrzenią B, lub może być traktowana jako przestrzeń B, albo zapewnia przestrzeń B -kosmiczna, itd. Leczenie a i B klas przestrzeni można interpretować strzałkę jako przejście z punktu a do B. (W kategoriach Bourbakiego męska „procedurę do odliczenia” z B-przestrzeni ze a-przestrzeni. Nie dość funkcji, chyba że klasy A, B są ustawione ; ten niuans nie unieważnia następujących.) Dwie strzałki na rys. 3 nie są odwracalne, ale z różnych powodów.

Przejście od „euklidesowego” do „topologicznego” jest zapominalskie. Topologia rozróżnia ciągłość od nieciągłości, ale nie rozróżnia prostoliniowej od krzywoliniowej. Intuicja podpowiada nam, że struktury euklidesowej nie można odtworzyć z topologii. Dowód wykorzystuje automorfizm przestrzeni topologicznej (tj. autohomeomorfizm ), który nie jest automorfizmem przestrzeni euklidesowej (tj. nie jest kompozycją przesunięć, obrotów i odbić). Taka transformacja zmienia daną strukturę euklidesową w (izomorficzną, ale) inną strukturę euklidesową; obie struktury euklidesowe odpowiadają jednej strukturze topologicznej.

W przeciwieństwie do tego przejście od „3-słabego euklidesowego” do „euklidesowego” nie jest zapominane; Przestrzeń euklidesowa nie musi być trójwymiarowa, ale jeśli jest trójwymiarowa, to jest w pełni rozwinięta, żadna struktura nie jest tracona. Innymi słowy, to drugie przejście jest iniektywne (jeden do jednego), podczas gdy pierwsze przejście nie jest iniektywne (wiele do jednego). Przejścia iniektywne oznaczamy strzałką z zadziorem, „↣” zamiast „→”.

Oba przejścia nie są surjektywne , to znaczy nie każda przestrzeń B wynika z jakiejś przestrzeni A. Po pierwsze, trójwymiarowa przestrzeń euklidesowa jest szczególnym (nie ogólnym) przypadkiem przestrzeni euklidesowej. Po drugie, topologia przestrzeni euklidesowej jest szczególnym przypadkiem topologii (na przykład musi być niezwarta i połączona itd.). Przejścia surjektywne oznaczamy strzałką z dwoma grotami, „↠” zamiast „→”. Zobacz na przykład rys. 4; tam strzałka od „rzeczywistej topologii liniowej” do „rzeczywistej liniowej” jest dwugłowa, ponieważ każda rzeczywista przestrzeń liniowa dopuszcza pewną (przynajmniej jedną) topologię zgodną z jej liniową strukturą.

Taka topologia jest ogólnie nieunikalna, ale unikalna, gdy rzeczywista przestrzeń liniowa jest skończenie wymiarowa. Dla tych przestrzeni przejście jest zarówno iniektywne, jak i surjektywne, czyli bijektywne ; patrz strzałka od „skończenie-słaba rzeczywista liniowa topologiczna” do „skończenie-słaba rzeczywista liniowa” na rys. 4. Odwrotne przejście istnieje (i mogłoby być pokazane drugą strzałką do tyłu). Te dwa rodzaje struktur są więc równoważne. W praktyce nie ma rozróżnienia między równoważnymi gatunkami struktur. Struktury równoważne można traktować jako pojedynczą strukturę, co pokazuje duże pole na rys. 4.

Przejścia oznaczone strzałkami są zgodne z izomorfizmami. Oznacza to, że dwie izomorficzne przestrzenie A prowadzą do dwóch izomorficznych przestrzeni B .

Schemat na rys. 4 jest przemienny . Oznacza to, że wszystkie skierowane ścieżki na diagramie z tym samym punktem początkowym i końcowym prowadzą do tego samego wyniku. Inne diagramy poniżej są również przemienne, z wyjątkiem strzałek przerywanych na ryc. 9. Strzałka od „topologicznego” do „mierzalnego” jest przerywana z wyjaśnionego tam powodu: „Aby zamienić przestrzeń topologiczną w mierzalną, wyposaża się ją w σ-algebra. σ-algebra zbiorów borelowskich jest najpopularniejszą, ale nie jedyną opcją." Wypełniona strzałka oznacza powszechne, tak zwane „kanoniczne” przejście, które sugeruje się naturalnie i jest powszechnie używane, często domyślnie, domyślnie. Mówiąc na przykład o funkcji ciągłej w przestrzeni euklidesowej, nie trzeba jednoznacznie określać jej topologii. W rzeczywistości istnieją alternatywne topologie i czasami są używane, na przykład topologia precyzyjna ; ale są one zawsze wyraźnie określone, ponieważ są znacznie mniej godne uwagi niż dominująca topologia. Przerywana strzałka wskazuje, że w użyciu jest kilka przejść i żadna nie jest dość rozpowszechniona.

Rodzaje przestrzeni

Przestrzenie liniowe i topologiczne

Dwie podstawowe przestrzenie to przestrzenie liniowe (zwane również przestrzeniami wektorowymi) oraz przestrzenie topologiczne .

Przestrzenie liniowe mają charakter algebraiczny ; istnieje rzeczywiste miejsca liniowych (w ciągu zakresie od liczb rzeczywistych ), kompleks przestrzenie liniowe (powyżej zakresie liczb zespolonych ), a bardziej ogólnie, przestrzenie liniowe w każdym polu. Każda złożona przestrzeń liniowa jest również rzeczywistą przestrzenią liniową (ta druga leży u podstaw pierwszej), ponieważ każda liczba rzeczywista jest również liczbą zespoloną. Mówiąc bardziej ogólnie, przestrzeń wektorowa nad ciałem ma również strukturę przestrzeni wektorowej nad podciałem tego pola. Operacje liniowe, podane w przestrzeni liniowej, z definicji prowadzą do takich pojęć, jak linie proste (i płaszczyzny i inne podprzestrzenie liniowe); równoległe linie; elipsy (i elipsoidy). Nie da się jednak zdefiniować linii ortogonalnych (prostopadłych), ani wyodrębnić okręgów między elipsami, ponieważ w przestrzeni liniowej nie ma struktury typu iloczyn skalarny, który można by wykorzystać do pomiaru kątów. Wymiar przestrzeni liniowej jest definiowany jako maksymalna liczba liniowo niezależnych wektorów lub równoważnie jako minimalna liczba wektorów obejmujących przestrzeń; może być skończony lub nieskończony. Dwie przestrzenie liniowe nad tym samym polem są izomorficzne wtedy i tylko wtedy, gdy mają ten sam wymiar. N wymiarową kompleks przestrzeń liniowa jest także 2 n wymiarową rzeczywistą przestrzeń liniowa.

Przestrzenie topologiczne mają charakter analityczny . Zbiory otwarte , podane w przestrzeni topologicznej z definicji, prowadzą do takich pojęć jak funkcje ciągłe , ścieżki, mapy; ciągi zbieżne, granice ; wnętrze, granica, zewnętrzna. Jednak jednostajna ciągłość , zbiory ograniczone , ciągi Cauchy'ego , funkcje różniczkowalne (ścieżki, mapy) pozostają niezdefiniowane. Izomorfizmy pomiędzy przestrzeniami topologicznymi tradycyjnie nazywa się homeomorfizmami; są to korespondencje jeden do jednego, ciągłe w obu kierunkach. Otwarty przedział (0,1) jest homeomorficzny całej prostej (-∞, ∞), ale nie homeomorficzny do zamkniętego przedziału [0,1], ani koła. Powierzchnia sześcianu jest homeomorficzna dla kuli (powierzchnia kuli), ale nie homeomorficzna dla torusa. Przestrzenie euklidesowe o różnych wymiarach nie są homeomorficzne, co wydaje się oczywiste, ale niełatwe do udowodnienia. Wymiar przestrzeni topologicznej jest trudny do zdefiniowania; można zastosować wymiar indukcyjny (na podstawie obserwacji, że wymiar granicy figury geometrycznej jest zwykle o jeden mniejszy od wymiaru samej figury) oraz wymiar pokrycia Lebesgue'a . W przypadku n- wymiarowej przestrzeni euklidesowej oba wymiary topologiczne są równe n .

Każdy podzbiór przestrzeni topologicznej sam w sobie jest przestrzenią topologiczną (w przeciwieństwie do tego, tylko liniowe podzbiory przestrzeni liniowej są przestrzeniami liniowymi). Arbitralne przestrzenie topologiczne, badane przez topologię ogólną (nazywaną również topologią zbioru punktów) są zbyt zróżnicowane, aby można było dokonać pełnej klasyfikacji aż do homeomorfizmu. Zwarte przestrzenie topologiczne są ważną klasą przestrzeni topologicznych („gatunki” tego „typu”). Każda funkcja ciągła jest ograniczona do takiej przestrzeni. Domknięty przedział [0,1] i rozszerzona prosta rzeczywista [−∞,∞] są zwarte; przedział otwarty (0,1) i linia (−∞,∞) nie są. Topologia geometryczna bada rozmaitości (inny „gatunek” tego „typu”); są to przestrzenie topologiczne lokalnie homeomorficzne z przestrzeniami euklidesowymi (i spełniające kilka dodatkowych warunków). Rozmaitości niskowymiarowe są całkowicie zaklasyfikowane do homeomorfizmu.

Zarówno struktura liniowa, jak i topologiczna leżą u podstaw struktury liniowej przestrzeni topologicznej (inaczej mówiąc topologicznej przestrzeni wektorowej). Liniowa przestrzeń topologiczna to zarówno rzeczywista lub złożona przestrzeń liniowa, jak i przestrzeń topologiczna, tak że operacje liniowe są ciągłe. Zatem przestrzeń liniowa, która jest również topologiczna, nie jest na ogół liniową przestrzenią topologiczną.

Każda skończenie wymiarowa rzeczywista lub złożona przestrzeń liniowa jest liniową przestrzenią topologiczną w tym sensie, że zawiera jedną i tylko jedną topologię, która czyni ją liniową przestrzenią topologiczną. Te dwie struktury, „skończenie wymiarowa rzeczywista lub złożona przestrzeń liniowa” i „skończenie wymiarowa liniowa przestrzeń topologiczna”, są zatem równoważne, to znaczy wzajemnie leżące. W związku z tym każda odwracalna transformacja liniowa skończenie wymiarowej liniowej przestrzeni topologicznej jest homeomorfizmem. Trzy pojęcia wymiaru (jeden algebraiczny i dwa topologiczne) zgadzają się dla skończenie wymiarowych rzeczywistych przestrzeni liniowych. Jednak w przestrzeniach nieskończenie wymiarowych różne topologie mogą być zgodne z daną strukturą liniową, a odwracalne przekształcenia liniowe generalnie nie są homeomorfizmami.

Przestrzenie afiniczne i rzutowe

Wygodnie jest wprowadzić przestrzenie afiniczne i rzutowe za pomocą przestrzeni liniowych w następujący sposób. N wymiarową liniowy podprzestrzeń ( n + 1) wymiarowej przestrzeni liniowej, jest sama w sobie n wymiarową przestrzeń liniowa, nie jest jednorodna; zawiera specjalny punkt, początek. Przesuwając ją o wektor zewnętrzny względem niej, otrzymujemy n- wymiarową podprzestrzeń afiniczną. Jest jednorodny. Przestrzeń afiniczna nie musi być zawarta w przestrzeni liniowej, ale jest izomorficzna z podprzestrzenią afiniczną przestrzeni liniowej. Wszystkie n- wymiarowe przestrzenie afiniczne są wzajemnie izomorficzne. Mówiąc słowami Johna Baeza , „przestrzeń afiniczna to przestrzeń wektorowa, która zapomniała o swoim pochodzeniu”. W szczególności każda przestrzeń liniowa jest również przestrzenią afiniczną.

Mając n- wymiarową podprzestrzeń afiniczną A w ( n +1)-wymiarowej przestrzeni liniowej L , linię prostą w A można zdefiniować jako przecięcie przestrzeni A z dwuwymiarową podprzestrzenią liniową L, która przecina A : innymi słowy , z płaszczyzną przechodzącą przez początek, która nie jest równoległa do A . Bardziej ogólnie, k- wymiarowa podprzestrzeń afiniczna A jest przecięciem przestrzeni A z ( k +1)-wymiarową podprzestrzenią liniową przestrzeni L, która przecina A .

Każdy punkt podprzestrzeni afinicznej A jest przecięciem przestrzeni A z jednowymiarową podprzestrzenią liniową przestrzeni L . Jednak niektóre jednowymiarowe podprzestrzenie L są równoległe do A ; w pewnym sensie przecinają A w nieskończoności. Zbiór wszystkich jednowymiarowych podprzestrzeni liniowych ( n +1)-wymiarowej przestrzeni liniowej jest z definicji n- wymiarową przestrzenią rzutową. A podprzestrzeń afiniczna A jest osadzona w przestrzeni rzutowej jako właściwy podzbiór. Jednak sama przestrzeń projekcyjna jest jednorodna. Linia prosta w przestrzeni rzutowej odpowiada dwuwymiarowej liniowej podprzestrzeni ( n +1)-wymiarowej przestrzeni liniowej. Bardziej ogólnie, k- wymiarowa podprzestrzeń rzutowa przestrzeni rzutowej odpowiada ( k +1)-wymiarowej liniowej podprzestrzeni ( n +1)-wymiarowej przestrzeni liniowej i jest izomorficzna z k- wymiarową przestrzenią rzutową.

Tak zdefiniowane przestrzenie afiniczne i rzutowe mają charakter algebraiczny; mogą być rzeczywiste, złożone i bardziej ogólnie, w dowolnej dziedzinie.

Każda rzeczywista lub złożona przestrzeń afiniczna lub rzutowa jest również przestrzenią topologiczną. Przestrzeń afiniczna jest rozmaitością niezwartą; przestrzeń rzutowa jest zwartą rozmaitością. W rzeczywistej przestrzeni rzutowej linia prosta jest homeomorficzna z okręgiem, a więc zwarta, w przeciwieństwie do linii prostej w liniowości przestrzeni afinicznej.

Przestrzenie metryczne i jednolite

Odległości między punktami są definiowane w przestrzeni metrycznej . Izomorfizmy pomiędzy przestrzeniami metrycznymi nazywamy izometriami. Każda przestrzeń metryczna jest również przestrzenią topologiczną. Przestrzeń topologiczna nazywana jest metryzowalną , jeśli leży u podstaw przestrzeni metrycznej. Wszystkie kolektory są metryzowalne.

W przestrzeni metrycznej możemy zdefiniować zbiory ograniczone i ciągi Cauchy'ego. Przestrzeń metryczna nazywana jest kompletną, jeśli wszystkie sekwencje Cauchy'ego są zbieżne. Każda niekompletna przestrzeń jest izometrycznie osadzona, jako gęsty podzbiór, w pełnej przestrzeni (dopełnienie). Każda kompaktowa przestrzeń metryczna jest kompletna; prawdziwa linia nie jest zwarta, ale kompletna; przedział otwarty (0,1) jest niepełny.

Każda przestrzeń euklidesowa jest również pełną przestrzenią metryczną. Co więcej, wszystkie pojęcia geometryczne immanentne przestrzeni euklidesowej można scharakteryzować pod względem metryki. Na przykład odcinek prosty łączący dwa dane punkty A i C składa się ze wszystkich punktów B takich, że odległość między A i C jest równa sumie dwóch odległości, między A i B oraz między B i C .

Wymiar Hausdorffa (w odniesieniu do liczby małych kulek, które obejmują dany zestaw) odnosi się do przestrzeni metrycznych, a może być nie jest liczbą całkowitą (szczególnie dla fraktale ). Dla n- wymiarowej przestrzeni euklidesowej wymiar Hausdorffa jest równy n .

Przestrzenie jednorodne nie wprowadzają odległości, ale nadal pozwalają na użycie jednostajnej ciągłości, ciągów Cauchy'ego (lub filtrów lub sieci ), kompletności i dopełniania. Każda jednolita przestrzeń jest również przestrzenią topologiczną. Każda liniowa przestrzeń topologiczna (metryzowalna lub nie) jest również przestrzenią jednorodną i jest zupełna w wymiarze skończonym, ale generalnie niekompletna w wymiarze nieskończonym. Mówiąc ogólniej, każda przemienna grupa topologiczna jest również jednolitą przestrzenią. Nieprzemienna grupa topologiczna ma jednak dwie jednolite struktury, jedną lewostronną, a drugą prawostronną.

Przestrzenie znormalizowane, Banacha, iloczyn skalarny i przestrzenie Hilberta

Wektory w przestrzeni euklidesowej tworzą przestrzeń liniową, ale każdy wektor ma również długość, czyli normę, . Rzeczywista lub złożona przestrzeń liniowa wyposażona w normę jest przestrzenią unormowaną . Każda przestrzeń unormowana jest zarówno liniową przestrzenią topologiczną, jak i przestrzenią metryczną. Przestrzeń Banacha jest kompletnym Normed przestrzeń. Wiele przestrzeni ciągów lub funkcji jest nieskończenie wymiarowymi przestrzeniami Banacha. ${\displaystyle x}$${\ Displaystyle \ lVert x \ rVert}$

Zbiór wszystkich wektorów o normie mniejszej niż jeden nazywany jest kulą jednostkową przestrzeni unormowanej. Jest to zestaw wypukły, centralnie symetryczny, na ogół nie elipsoida; na przykład może to być wielokąt (w płaszczyźnie) lub, bardziej ogólnie, wielokąt (w dowolnym wymiarze skończonym). Prawo równoległoboku (zwane również tożsamością równoległoboku)

${\ Displaystyle \ l Vert xy \ r Vert ^ {2} + \ l Vert x + y \ r Vert ^ {2} = 2 \ l Vert x \ r Vert ^ {2} + 2 \ l Vert y \ r Vert ^ {2} \ ,}$

generalnie zawodzi w przestrzeniach unormowanych, ale obowiązuje dla wektorów w przestrzeniach euklidesowych, co wynika z faktu, że kwadrat normy euklidesowej wektora jest jego iloczynem wewnętrznym z samym sobą, . ${\ Displaystyle \ lVert x \ rVert ^ {2} = (x, x)}$

Przestrzeń produktu skalarnego to rzeczywista lub złożona przestrzeń liniowa, obdarzona formą dwuliniową lub odpowiednio półtoraliniową, spełniająca pewne warunki i nazywana iloczynem skalarnym. Każda wewnętrzna przestrzeń produktowa jest również przestrzenią unormowaną. Przestrzeń unormowana leży u podstaw przestrzeni produktu wewnętrznego wtedy i tylko wtedy, gdy spełnia prawo równoległoboku lub równoważnie, jeśli jego kula jednostkowa jest elipsoidą. Kąty pomiędzy wektorami są zdefiniowane w wewnętrznych przestrzeniach produktowych. Przestrzeń Hilberta jest zdefiniowana jako kompletny wewnętrznej powierzchni produktu. (Niektórzy autorzy twierdzą, że musi być złożona, inni przyznają również rzeczywiste przestrzenie Hilberta.) Wiele przestrzeni sekwencji lub funkcji jest nieskończenie wymiarowymi przestrzeniami Hilberta. Przestrzenie Hilberta są bardzo ważne dla teorii kwantowej .

Wszystkie n- wymiarowe rzeczywiste wewnętrzne przestrzenie produktowe są wzajemnie izomorficzne. Można powiedzieć, że n- wymiarowa przestrzeń euklidesowa jest n- wymiarową realną przestrzenią produktu wewnętrznego, która zapomniała o swoim pochodzeniu.

Rozmaitości gładkie i riemannowskie

Rozmaitości gładkie nie są nazywane „przestrzeniami”, ale mogą nimi być. Każda gładka rozmaitość jest rozmaitością topologiczną i może być osadzona w skończenie wymiarowej przestrzeni liniowej. Gładkie powierzchnie w skończenie wymiarowej przestrzeni liniowej są gładkimi rozmaitościami: na przykład powierzchnia elipsoidy jest gładką rozmaitością, a polytope nie. Rzeczywiste lub złożone skończenie wymiarowe przestrzenie liniowe, afiniczne i rzutowe są również gładkimi rozmaitościami.

W każdym ze swoich punktów gładka ścieżka w gładkiej rozmaitości ma wektor styczny należący do przestrzeni stycznej tej rozmaitości w tym punkcie. Przestrzenie styczne do n- wymiarowej gładkiej rozmaitości są n- wymiarowymi przestrzeniami liniowymi. Różniczka funkcji gładkiej na gładkiej rozmaitości zapewnia funkcję liniową na przestrzeni stycznej w każdym punkcie.

Riemanna kolektora lub przestrzeń Riemanna jest gładka kolektorze którego obowiązuje styczne są wyposażone w wewnętrzne produktów spełniających pewne warunki. Przestrzenie euklidesowe są również przestrzeniami Riemanna. Powierzchnie gładkie w przestrzeniach euklidesowych to przestrzenie Riemanna. Przestrzeń hiperboliczna nieeuklidesowa jest również przestrzenią Riemanna. Krzywa w przestrzeni Riemanna ma długość, a długość najkrótszej krzywej między dwoma punktami określa odległość tak, że przestrzeń Riemanna jest przestrzenią metryczną. Kąt między dwoma krzywymi przecinającymi się w punkcie to kąt między ich stycznymi.

Odkładając dodatniość iloczynów skalarnych na przestrzenie styczne, otrzymujemy przestrzenie pseudo-Riemanna , w tym przestrzenie Lorentza, które są bardzo ważne dla ogólnej teorii względności .

Przestrzenie mierzalne, miary i probabilistyczne

Rezygnując z odległości i kątów przy zachowaniu objętości (ciał geometrycznych) dochodzi się do teorii miary . Oprócz objętości, miara uogólnia pojęcia powierzchni, długości, rozkładu masy (lub ładunku), a także rozkładu prawdopodobieństwa, zgodnie z podejściem Andrieja Kołmogorowa do teorii prawdopodobieństwa .

„Ciało geometryczne” matematyki klasycznej jest znacznie bardziej regularne niż tylko zbiór punktów. Granica ciała ma zerową objętość. Zatem objętość ciała jest objętością jego wnętrza, a wnętrze może być wyczerpane przez nieskończoną sekwencję sześcianów. Natomiast granica dowolnego zbioru punktów może mieć niezerową objętość (przykład: zbiór wszystkich punktów wymiernych wewnątrz danego sześcianu). Teoria miary odniosła sukces w rozszerzeniu pojęcia objętości na szeroką klasę zbiorów, tak zwanych zbiorów mierzalnych . Rzeczywiście, zbiory niemierzalne prawie nigdy nie występują w aplikacjach.

Zbiory mierzalne, podane w mierzalnej przestrzeni, z definicji prowadzą do mierzalnych funkcji i map. W celu przekształcenia przestrzeni topologicznej w przestrzeń mierzalną wyposaża się ją w σ-algebrę. Σ-algebra z zbiór borelowski jest najbardziej popularne, ale nie jedynym wyborem. ( Zestawy Baire , Uniwersalnie mierzalnych , itp, są wykorzystywane często.) Topologia nie jest jednoznacznie określona przez Borel Ď-Algebra; na przykład topologia norm i słaba topologia na separowalnej przestrzeni Hilberta prowadzą do tej samej σ-algebry Borela . Nie każda σ-algebra jest σ-algebrą borelowską jakiejś topologii. W rzeczywistości σ-algebrę można wygenerować przez dany zbiór zbiorów (lub funkcji) niezależnie od topologii. Każdy podzbiór przestrzeni mierzalnej sam w sobie jest przestrzenią mierzalną.

Standardowe przestrzenie mierzalne (nazywane również standardowymi przestrzeniami borelowskimi ) są szczególnie przydatne ze względu na pewne podobieństwo do przestrzeni zwartych (zobacz EoM ). Każde bijekcyjne mierzalne odwzorowanie pomiędzy standardowymi mierzalnymi przestrzeniami jest izomorfizmem; oznacza to, że mapowanie odwrotne jest również mierzalne. A odwzorowanie między takimi przestrzeniami jest mierzalne wtedy i tylko wtedy, gdy jego wykres jest mierzalny w przestrzeni produktu. Podobnie, każde bijective ciągłe mapowanie pomiędzy zwartymi przestrzeniami metrycznymi jest homeomorfizmem; oznacza to, że odwzorowanie odwrotne jest również ciągłe. A odwzorowanie między takimi przestrzeniami jest ciągłe wtedy i tylko wtedy, gdy jego graf jest zamknięty w przestrzeni produktu.

Każdy zbiór borelowski w przestrzeni euklidesowej (a bardziej ogólnie w całkowicie odzielnej przestrzeni metrycznej), wyposażony w algebrę borelowską σ, jest standardową przestrzenią mierzalną. Wszystkie niepoliczalne standardowe przestrzenie mierzalne są wzajemnie izomorficzne.

Przestrzeń miarą jest mierzalna przestrzeń obdarzona środka. Przestrzeń euklidesowa z miarą Lebesgue'a jest przestrzenią miary. Teoria całkowania definiuje całkowalność i całki funkcji mierzalnych na przestrzeni miar.

Zbiory miary 0, zwane zestawami zerowymi, są pomijalne. W związku z tym „izomorfizm mod 0” jest definiowany jako izomorfizm między podzbiorami pełnej miary (to znaczy z pomijalnym dopełnieniem).

Przestrzeń prawdopodobieństwo jest przestrzeń środek taki, że środek całej powierzchni jest równe 1. Produkt z każdej rodziny (Finite lub nie) przestrzeni prawdopodobieństwo przestrzeń prawdopodobieństwa. W przeciwieństwie do tego, dla przestrzeni miar w ogóle, definiowany jest tylko iloczyn skończenie wielu przestrzeni. W związku z tym istnieje wiele nieskończeniewymiarowych miar prawdopodobieństwa (zwłaszcza miary Gaussa ), ale nie ma nieskończeniewymiarowych miar Lebesgue'a.

Szczególnie przydatne są standardowe przestrzenie prawdopodobieństwa . Na standardowej przestrzeni prawdopodobieństwa warunkowe oczekiwanie może być traktowane jako całka po mierze warunkowej ( regularne prawdopodobieństwa warunkowe , zobacz też rozpad miary ). Biorąc pod uwagę dwie standardowe przestrzenie prawdopodobieństwa, każdy homomorfizm ich algebr miar jest indukowany przez pewną miarę zachowującą mapę. Każda miara prawdopodobieństwa na standardowej mierzalnej przestrzeni prowadzi do standardowej przestrzeni prawdopodobieństwa. Iloczynem ciągu (skończonego lub nie) standardowych przestrzeni prawdopodobieństwa jest standardowa przestrzeń prawdopodobieństwa. Wszystkie nieatomowe standardowe przestrzenie prawdopodobieństwa są wzajemnie izomorficzne mod 0; jednym z nich jest przedział (0,1) z miarą Lebesgue'a.

Te przestrzenie są mniej geometryczne. W szczególności idea wymiaru, która ma zastosowanie (w takiej czy innej formie) do wszystkich innych przestrzeni, nie ma zastosowania do przestrzeni mierzalnych, miar i prawdopodobieństwa.

Nieprzemienna geometria

Teoretyczne badanie rachunku różniczkowego, znane jako analiza matematyczna , doprowadziło na początku XX wieku do rozważenia liniowych przestrzeni funkcji o wartościach rzeczywistych lub zespolonych. Najwcześniejszymi ich przykładami były przestrzenie funkcyjne , każda dostosowana do własnej klasy problemów. Przykłady te miały wiele wspólnych cech, które wkrótce zostały wyodrębnione w przestrzenie Hilberta, przestrzenie Banacha i bardziej ogólne topologiczne przestrzenie wektorowe. Były to potężne narzędzia do rozwiązywania szerokiego zakresu problemów matematycznych.

Najbardziej szczegółowe informacje przyniosła klasa przestrzeni zwana algebrami Banacha . Są to przestrzenie Banacha wraz z ciągłą operacją mnożenia. Ważnym wczesnym przykładem była algebra Banacha zasadniczo ograniczonych funkcji mierzalnych na przestrzeni miary X . Ten zbiór funkcji to przestrzeń Banacha z dodawaniem punktowym i mnożeniem przez skalar. Dzięki operacji mnożenia punktowego staje się ona szczególnym typem przestrzeni Banacha, obecnie nazywanej przemienną algebrą von Neumanna . Mnożenie punktowe wyznacza reprezentację tej algebry na przestrzeni Hilberta funkcji całkowalnych z kwadratem na X . Wczesną obserwacją Johna von Neumanna było to, że ta korespondencja działała również w odwrotnej kolejności: biorąc pod uwagę pewne łagodne hipotezy techniczne, przemienna algebra von Neumanna wraz z reprezentacją na przestrzeni Hilberta wyznacza przestrzeń miary, a te dwie konstrukcje (algebry von Neumanna plus reprezentacja i przestrzeń miary) są wzajemnie odwrotne.

Von Neumann zaproponował następnie, że nieprzemienne algebry von Neumanna powinny mieć znaczenie geometryczne, tak jak robią to przemienne algebry von Neumanna. Wraz z Francisem Murrayem opracował klasyfikację algebr von Neumanna. Te bezpośrednie integralne pokazy budowlanych jak złamać żadnej algebry von Neumanna na zbiór prostych algebr zwanych czynnikami . Von Neumann i Murray podzielili czynniki na trzy typy. Typ I był prawie identyczny z przypadkiem przemiennym. Typy II i III wykazywały nowe zjawiska. Algebra von Neumanna typu II określiła geometrię ze szczególną cechą, że wymiarem może być dowolna nieujemna liczba rzeczywista, a nie tylko liczba całkowita. Algebry typu III to te, które nie były ani typu I, ani II, a po kilkudziesięciu latach pracy udowodniono, że są one blisko związane z czynnikami typu II.

Nieco inne podejście do geometrii przestrzeni funkcyjnych rozwinęło się w tym samym czasie co prace von Neumanna i Murraya dotyczące klasyfikacji czynników. To podejście jest teorią C*-algebr . Tutaj motywującym przykładem jest C*-algebra , gdzie X jest lokalnie zwartą przestrzenią topologiczną Hausdorffa. Z definicji jest to algebra ciągłych funkcji o wartościach zespolonych na X, które zanikają w nieskończoności (co luźno oznacza, że ​​im dalej od wybranego punktu, tym funkcja zbliża się do zera) z operacjami dodawania i mnożenia punktów. Twierdzenie Gelfanda-Naimarka implikowało, że istnieje zgodność między przemiennymi C*-algebrami a obiektami geometrycznymi: Każda przemienna C*-algebra ma postać pewnej lokalnie zwartej przestrzeni X Hausdorffa . W konsekwencji możliwe jest badanie lokalnie zwartych przestrzeni Hausdorffa wyłącznie w kategoriach przemiennych C*-algebr. Nieprzemienna geometria bierze to za inspirację do badania nieprzemiennych C*-algebr: Gdyby istniało coś takiego jak „nieprzemienna przestrzeń X ”, to byłaby to nieprzemienna C*-algebra ; jeśli dodatkowo twierdzenie Gelfanda-Naimarka zastosowane do tych nieistniejących obiektów, to przestrzenie (przemienne lub nie) byłyby takie same jak C*-algebry; tak więc, z powodu braku bezpośredniego podejścia do definicji przestrzeni nieprzemiennej, przestrzeń nieprzemienna jest definiowana jako nieprzemienna C*-algebra. Wiele standardowych narzędzi geometrycznych można przeformułować w kategoriach C*-algebr, co daje inspirowane geometrią techniki badania nieprzemiennych C*-algebr . ${\displaystyle C_{0}(X)}$${\displaystyle C_{0}(X)}$${\displaystyle C_{0}(X)}$

Oba te przykłady są teraz przypadkami pola zwanego geometrią nieprzemienną . Konkretne przykłady algebr von Neumanna i C*-algebr są znane odpowiednio jako nieprzemienna teoria miary i nieprzemienna topologia. Geometria nieprzemienna nie jest jedynie dążeniem do ogólności dla samego siebie i nie jest tylko ciekawostką. Przestrzenie nieprzemienne powstają naturalnie, a nawet nieuchronnie, z niektórych konstrukcji. Rozważmy na przykład nieokresowe kafelki Penrose'a samolotu za pomocą latawców i rzutek. Jest to twierdzenie, że w takim kafelku każdy skończony kawałek latawców i rzutek pojawia się nieskończenie często. W konsekwencji nie można odróżnić dwóch płytek Penrose patrząc na skończoną porcję. Uniemożliwia to przypisanie zbiorowi wszystkich kafelków topologii w tradycyjnym sensie. Mimo to kafelki Penrose'a wyznaczają nieprzemienną C*-algebrę, a co za tym idzie, mogą być badane za pomocą technik geometrii nieprzemiennej. Inny przykład, bardzo interesujący w geometrii różniczkowej , pochodzi z foliacji rozmaitości. Są to sposoby dzielenia rozmaitości na mniejsze podrozmaitości, zwane liśćmi , z których każdy jest lokalnie równoległy do ​​innych znajdujących się w pobliżu. Zbiór wszystkich liści można skomponować w przestrzeń topologiczną. Jednak przykład rotacji irracjonalnej pokazuje, że ta topologiczna przestrzeń może być niedostępna dla technik klasycznej teorii miary. Istnieje jednak nieprzemienna algebra von Neumanna związana z przestrzenią liścia foliacji, która ponownie daje niezrozumiałej w inny sposób przestrzeni dobrą strukturę geometryczną.

Schematy

Geometria algebraiczna bada właściwości geometryczne równań wielomianowych . Wielomiany to typ funkcji zdefiniowany z podstawowych operacji arytmetycznych dodawania i mnożenia. Z tego powodu są ściśle związane z algebrą. Geometria algebraiczna oferuje sposób na zastosowanie technik geometrycznych do pytań z czystej algebry i na odwrót.

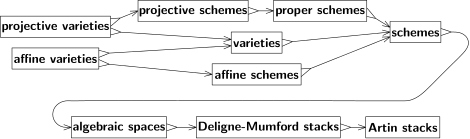
Przed latami czterdziestymi geometria algebraiczna działała wyłącznie na liczbach zespolonych, a najbardziej podstawową odmianą była przestrzeń rzutowa. Geometria przestrzeni rzutowej jest ściśle związana z teorią perspektywy , a jej algebra jest opisana wielomianami jednorodnymi . Wszystkie inne odmiany zostały zdefiniowane jako podzbiory przestrzeni rzutowej. Odmiany rzutowe były podzbiorami zdefiniowanymi przez zbiór wielomianów jednorodnych. W każdym punkcie rozmaitości rzutowej wszystkie wielomiany w zbiorze musiały być równe zeru. Dopełnieniem zbioru zerowego wielomianu liniowego jest przestrzeń afiniczna, a rozmaitość afiniczna była przecięciem rozmaitości rzutowej z przestrzenią afiniczną.

André Weil zauważył, że rozumowanie geometryczne można czasem zastosować w sytuacjach opartych na teorii liczb, gdzie rozpatrywane przestrzenie mogą być dyskretne lub nawet skończone. Realizując ten pomysł, Weil przepisał podstawy geometrii algebraicznej, zarówno uwalniając geometrię algebraiczną od jej zależności od liczb zespolonych, jak i wprowadzając abstrakcyjne rozmaitości algebraiczne, które nie były osadzone w przestrzeni rzutowej. Są to teraz po prostu odmiany .

Typ przestrzeni leżący u podstaw współczesnej geometrii algebraicznej jest jeszcze bardziej ogólny niż abstrakcyjne rozmaitości algebraiczne Weila. Został wprowadzony przez Aleksandra Grothendiecka i nosi nazwę schematu . Jedną z motywacji teorii schematów jest to, że wielomiany mają niezwykłą strukturę między funkcjami, a rozmaitości algebraiczne są w konsekwencji sztywne. To stwarza problemy przy próbie badania zdegenerowanych sytuacji. Na przykład prawie każda para punktów na okręgu wyznacza unikalną linię zwaną sieczną, a gdy dwa punkty poruszają się po okręgu, sieczna linia zmienia się w sposób ciągły. Jednak gdy te dwa punkty zderzają się, sieczna linia degeneruje się do linii stycznej. Linia styczna jest unikalna, ale geometria tej konfiguracji — pojedynczy punkt na okręgu — nie jest wystarczająco wyrazista, aby określić jednoznaczną linię. Badanie takich sytuacji wymaga teorii zdolnej do przypisania dodatkowych danych do zdegenerowanych sytuacji.

Jednym z elementów składowych schematu jest przestrzeń topologiczna. Przestrzenie topologiczne mają funkcje ciągłe, ale funkcje ciągłe są zbyt ogólne, aby odzwierciedlać leżącą u ich podstaw strukturę algebraiczną. Innym składnikiem schematu jest zatem snop w przestrzeni topologicznej, zwany „snopem struktury”. Na każdym otwartym podzbiorze przestrzeni topologicznej snop określa zbiór funkcji zwanych „funkcjami regularnymi”. Przestrzeń topologiczna i snop struktury razem muszą spełniać warunki, które oznaczają, że funkcje pochodzą z operacji algebraicznych.

Podobnie jak rozmaitości, schematy są definiowane jako przestrzenie lokalnie modelowane na znanej przestrzeni. W przypadku rozmaitości znaną przestrzenią jest przestrzeń euklidesowa. W przypadku schematu modele lokalne nazywane są schematami afinicznymi . Schematy afiniczne zapewniają bezpośrednie połączenie między geometrią algebraiczną a algebrą przemienną . Podstawowym przedmiotem badań algebry przemiennej są pierścienie przemienne . Jeśli jest pierścieniem przemiennym, to istnieje odpowiedni schemat afiniczny, który przekłada strukturę algebraiczną na geometrię. I odwrotnie, każdy schemat afiniczny określa pierścień przemienny, a mianowicie pierścień globalnych odcinków jego snopa struktury. Te dwie operacje są wzajemnie odwrotne, więc schematy afiniczne dostarczają nowego języka do badania pytań w algebrze przemiennej. Z definicji każdy punkt w schemacie ma otwarte sąsiedztwo, które jest schematem afinicznym. ${\ Displaystyle R}$${\ Displaystyle \ Operatorname {Spec} R}$${\ Displaystyle R}$

Istnieje wiele schematów, które nie są powiązane. W szczególności przestrzenie rzutowe spełniają warunek zwany poprawnością, analogiczny do zwartości. Schematy afiniczne nie mogą być poprawne (poza trywialnymi sytuacjami, np. gdy schemat ma tylko jeden punkt), a zatem żadna przestrzeń rzutowa nie jest schematem afinicznym (z wyjątkiem zerowymiarowych przestrzeni rzutowych). Schematy rzutowe, czyli te, które powstają jako zamknięte podschematy przestrzeni rzutowej, to najważniejsza rodzina schematów.

Wprowadzono kilka uogólnień schematów. Michael Artin zdefiniował przestrzeń algebraiczną jako iloraz schematu przez relacje równoważności, które definiują morfizmy etalne . Przestrzenie algebraiczne zachowują wiele użytecznych właściwości schematów, a jednocześnie są bardziej elastyczne. Na przykład twierdzenie Keela-Mori może być użyte do wykazania, że ​​wiele przestrzeni moduli to przestrzenie algebraiczne.

Bardziej ogólny niż przestrzeń algebraiczna jest stos Deligne'a-Mumforda . Stosy DM są podobne do schematów, ale dopuszczają osobliwości, których nie można opisać wyłącznie za pomocą wielomianów. Odgrywają taką samą rolę dla schematów, jak orbifoldy dla rozmaitości . Na przykład iloraz płaszczyzny afinicznej przez skończoną grupę obrotów wokół początku daje stos Deligne'a-Mumforda, który nie jest schematem ani przestrzenią algebraiczną. Z dala od początku, iloraz akcji grupowej identyfikuje skończone zbiory równo rozmieszczonych punktów na okręgu. Ale na początku okrąg składa się tylko z jednego punktu, samego początku, a działanie grupowe ustala ten punkt. Jednak w ilorazowym stosie DM punkt ten zawiera dodatkowe dane dotyczące bycia ilorazem. Ten rodzaj wyrafinowanej struktury jest przydatny w teorii przestrzeni modułowych i faktycznie został pierwotnie wprowadzony do opisu modułów krzywych algebraicznych .

Kolejnym uogólnieniem są stosy algebraiczne , zwane również stosami Artina. Stosy DM są ograniczone do ilorazów przez skończone działania grupowe. Chociaż wystarcza to dla wielu problemów w teorii modułów, jest zbyt restrykcyjne dla innych, a stosy Artina pozwalają na bardziej ogólne iloraz.

Topoi

W pracy Grothendiecka nad przypuszczeniami Weila wprowadził nowy typ topologii, obecnie nazywany topologią Grothendiecka . Przestrzeń topologiczna (w zwykłym sensie) aksjomatyzuje pojęcie „bliskości”, czyniąc dwa punkty blisko siebie wtedy i tylko wtedy, gdy leżą w wielu takich samych zbiorach otwartych. Natomiast topologia Grothendiecka aksjomatyzuje pojęcie „pokrywania”. Pokrycie przestrzeni to zbiór podprzestrzeni, które łącznie zawierają wszystkie informacje o otaczającej przestrzeni. Ponieważ snopy są definiowane w kategoriach pokrycia, topologia Grothendiecka może być również postrzegana jako aksjomatyzacja teorii snopów.

Prace Grothendiecka nad swoimi topologiami doprowadziły go do teorii toposów . W swoich pamiętnikach Récoltes et Semailles nazwał je swoją „największą koncepcją”. Snopek (w przestrzeni topologicznej lub w odniesieniu do topologii Grothendiecka) służy do wyrażania danych lokalnych. Kategoria wszystkich krążków wykonuje wszystkie możliwe sposoby wyrażania danych lokalnych. Ponieważ przestrzenie topologiczne zbudowane są z punktów, które same w sobie są rodzajem danych lokalnych, kategoria snopów może być zatem użyta jako zamiennik przestrzeni pierwotnej. Grothendieck konsekwentnie definiował topos jako kategorię snopów i badał topos jako samodzielne obiekty zainteresowania. Są to teraz toposy Grothendiecka .

Każda przestrzeń topologiczna wyznacza topos i odwrotnie. Istnieją przestrzenie topologiczne, w których pobranie powiązanych toposów powoduje utratę informacji, ale są one ogólnie uważane za patologiczne. (Warunkiem koniecznym i wystarczającym jest to, aby przestrzeń topologiczna była przestrzenią trzeźwą .) I odwrotnie, istnieją toposy, których skojarzone przestrzenie topologiczne nie obejmują pierwotnych toposów. Ale toposy te, dalekie od patologii, mogą być bardzo interesujące matematycznie. Na przykład teorię kohomologii etalnej Grothendiecka (która ostatecznie doprowadziła do potwierdzenia hipotez Weila) można sformułować jako kohomologię w etalnym toposu schematu, a topos ten nie pochodzi z przestrzeni topologicznej.

Przestrzenie topologiczne w rzeczywistości prowadzą do bardzo specjalnych toposów zwanych locales . Zbiór otwartych podzbiorów przestrzeni topologicznej wyznacza kratę . Aksjomaty przestrzeni topologicznej powodują, że te kraty są zupełnymi algebrami Heytinga . Teoria lokalizacji bierze to za punkt wyjścia. Locale definiuje się jako kompletną algebrę Heytinga, a elementarne właściwości przestrzeni topologicznych są ponownie wyrażane i udowadniane w tych terminach. Pojęcie locale okazuje się bardziej ogólne niż przestrzeń topologiczna, ponieważ każda trzeźwa przestrzeń topologiczna określa unikalne locale, ale wiele interesujących locale nie pochodzi z przestrzeni topologicznych. Ponieważ ustawienia regionalne nie muszą mieć punktów, badanie ustawień regionalnych jest nieco żartobliwie nazywane bezsensowną topologią .

Topoi wyświetla również głębokie powiązania z logiką matematyczną. Każdy topos Grothendiecka ma specjalny snopek zwany klasyfikatorem podobiektów. Ten klasyfikator podobiektów działa jak zbiór wszystkich możliwych wartości logicznych. W toposach zestawów klasyfikatorem podobiektów jest zestaw , odpowiadający wartościom „Fałsz” i „Prawda”. Ale w innych toposach klasyfikator podobiektów może być znacznie bardziej skomplikowany. Lawvere i Tierney uznali, że aksjomatyzacja klasyfikatora podobiektów dała bardziej ogólny rodzaj toposów, obecnie znany jako topos elementarny , i że elementarne toposy są modelami logiki intuicjonistycznej . Oprócz dostarczenia potężnego sposobu na zastosowanie narzędzi od logiki do geometrii, umożliwiło to wykorzystanie metod geometrycznych w logice. ${\ Displaystyle \ {0,1 \}}$

Przestrzenie i konstrukcje

Według Kevina Carlsona,

Żadne z tych słów ["przestrzeń" i "struktura"] nie ma jednej definicji matematycznej. Angielskie słowa mogą być używane w zasadniczo wszystkich tych samych sytuacjach, ale często myślisz o „przestrzeni” jako bardziej geometrycznej, a „strukturze” jako bardziej algebraicznej. [...] Można więc myśleć o „strukturach” jako miejscach, w których zajmujemy się algebrą, ao „przestrzeniach” jako miejscach, w których zajmujemy się geometrią. Następnie wiele wspaniałej matematyki powstało z przechodzenia od struktur do przestrzeni i odwrotnie, jak gdy patrzymy na podstawową grupę przestrzeni topologicznej lub widmo pierścienia . Ale ostatecznie rozróżnienie nie jest ani trudne, ani szybkie i idzie tylko tak daleko: wiele rzeczy to oczywiście zarówno struktury, jak i przestrzenie, niektóre rzeczy też nie są oczywiste, a niektórzy ludzie mogą się nie zgodzić ze wszystkim, co tutaj powiedziałem.

Niemniej jednak ogólna definicja „struktury” została zaproponowana przez Bourbaki; obejmuje wszystkie wymienione powyżej typy przestrzeni , (prawie?) wszystkie rodzaje struktur matematycznych stosowanych do tej pory i nie tylko. Podaje ogólną definicję izomorfizmu i uzasadnia przenoszenie własności pomiędzy strukturami izomorficznymi. Jednak nigdy nie był aktywnie wykorzystywany w praktyce matematycznej (nawet w traktatach matematycznych pisanych przez samego Bourbaki). Oto ostatnie zdania z recenzji książki Leo Corry'ego autorstwa Roberta Reeda:

Corry wydaje się nie sądzić, że jakakolwiek formalna definicja struktury mogłaby oddać sprawiedliwość używaniu tego pojęcia w rzeczywistej praktyce matematycznej [...] Pogląd Corry'ego można podsumować jako przekonanie, że „struktura” odnosi się zasadniczo do sposobu uprawiania matematyki , a zatem jest pojęciem prawdopodobnie równie dalekim od precyzyjnego zdefiniowania, jak kulturowy artefakt samej matematyki.

Więcej informacji na temat struktur matematycznych można znaleźć w Wikipedii: struktura matematyczna , równoważne definicje struktur matematycznych i transport struktury .

Rozróżnienie między „przestrzeniami” geometrycznymi a „strukturami” algebraicznymi jest czasami jasne, czasami nieuchwytne. Oczywiście grupy są algebraiczne, podczas gdy przestrzenie euklidesowe są geometryczne. Moduły nad pierścieniami są tak samo algebraiczne jak grupy. W szczególności, gdy pierścień wydaje się być polem , moduł wydaje się być przestrzenią liniową ; czy to algebraiczne czy geometryczne? W szczególności, gdy jest skończenie wymiarowa, ponad liczbami rzeczywistymi i obdarzona iloczynem wewnętrznym , staje się przestrzenią euklidesową ; teraz geometryczny. Pole (algebraiczne?) liczb rzeczywistych jest takie samo jak (geometryczna?) linia rzeczywista . Jego algebraiczne zamknięcie , (algebraiczne?) ciało liczb zespolonych , jest takie samo jak (geometryczna?) płaszczyzna zespolona . Jest to przede wszystkim „miejsce, w którym przeprowadzamy analizę ” (a nie algebra czy geometria).

Każda przestrzeń opisana w sekcji „ Typy przestrzeni ” powyżej, z wyjątkiem podsekcji „Geometria nieprzemienna”, „Schematy” i „Topoi”, jest zbiorem („główny zbiór bazowy” struktury, według Bourbakiego) wyposażonym w jakaś dodatkowa struktura; elementy zestawu podstawowego nazywane są zwykle „punktami” tej przestrzeni. W przeciwieństwie do tego, elementy (zbioru podstawowego) struktury algebraicznej zwykle nie są nazywane „punktami”.

Czasami jednak używa się więcej niż jednego podstawowego zestawu podstawowego. Na przykład dwuwymiarowa geometria rzutowa może być sformalizowana za pomocą dwóch zbiorów bazowych , zbioru punktów i zbioru linii. Ponadto uderzającą cechą płaszczyzn rzutowych jest symetria ról pełnionych przez punkty i linie . Mniej geometryczny przykład: graf można sformalizować za pomocą dwóch zbiorów bazowych , zbioru wierzchołków (zwanych również węzłami lub punktami) oraz zbioru krawędzi (zwanych również łukami lub liniami). Ogólnie rzecz biorąc, skończenie wiele podstawowych zestawów zasad i skończenie wiele pomocniczych zestawów zasad jest wymaganych przez Bourbaki.

Wiele matematycznych struktur geometrycznych omówionych w podrozdziałach „Nieprzemienna geometria”, „Schematy” i „Topoi” nie określa podstawowego zestawu punktów. Na przykład „ topologia bezcelowa ” (innymi słowy topologia bezpunktowa lub teoria lokalizacji) zaczyna się od pojedynczego zbioru bazowego, którego elementy imitują zbiory otwarte w przestrzeni topologicznej (ale nie są zbiorami punktów); zobacz także mereotopologia i geometria bezpunktowa .

Przestrzenie matematyczne według nazwy

Zobacz też

• Struktura matematyczna
• Transport konstrukcji
• Zestaw (matematyka)

Uwagi

Przypisy

Bibliografia

Ten artykuł został przesłany do WikiJournal of Science do zewnętrznej recenzji naukowej w 2017 r. ( raporty recenzentów ). Zaktualizowana treść została ponownie zintegrowana ze stroną Wikipedii na licencji CC-BY-SA-3.0 ( 2018 ). Recenzowana wersja zapisu to: Boris Tsirelson ; i in. (1 czerwca 2018). „Przestrzenie w matematyce” (PDF) . WikiJournal of Science . 1 (1): 2. doi : 10.15347/WJS/2018.002 . ISSN  2470-6345 . Wikidane  Q55120290 .

• Bourbaki, Nicolas , Elementy matematyki , Hermann (oryginał), Addison-Wesley (tłumaczenie).
• Bourbaki, Nicolas (1968), Elementy matematyki: Teoria zbiorów , Hermann (oryginał), Addison-Wesley (tłumaczenie).
• Eisenbud, Dawid; Harris, Joe (2000), Geometria schematów , Springer-Verlag, doi : 10.1007/b97680 , ISBN 978-0-387-98638-8.
• Gowers, Tymoteusz ; Barrow-Green, czerwiec; Lider, Imre , wyd. (2008), Princeton Companion to Mathematics , Princeton University Press, ISBN 978-0-691-11880-2.
• Itô, Kiyosi , wyd. (1993), Encyklopedyczny słownik matematyczny (wyd. drugie), Towarzystwo matematyczne Japonii (oryginał), prasa MIT (tłumaczenie).

Linki zewnętrzne

• Multimedia związane z kosmosem (matematyka) w Wikimedia Commons
• Matilde Marcolli (2009) Pojęcie przestrzeni w matematyce , z Caltech .